Учебно-методическое обеспечение лекции. Тема: неопределенный интеграл

Введение

ПЛАН ЛЕКЦИИ

Тема: Неопределенный интеграл

ЛЕКЦИЯ № 2

Чтения лекции № 2

ПЛАН

по дисциплине математика _ ___________________________

(наименование дисциплины)

Тема: Неопределенный интеграл ___

(наименование темы)

Цель занятия: о знакомление студентов с понятием неопределенного интеграла, его свойствами.

Литература по теме:

а) основная __1. Общий курс высшей математики для экономистов. Под ред. В.И. Ермакова. – М., 2010.

2. Кремер Н.Ш. Математика для экономистов. М.:ЮНИТИ- ДАНА, 2010.

№№ п.п.	Содержание занятия	Отводимое учебное время, мин.	Применяемые наглядные пособия и ТСО
	Организационная часть - проверить наличие студентов* Вводная часть (вступительное слово) - кратко напомнить материал предыдущего занятия; - объявить тему лекции; - довести учебные вопросы; - определить место темы в учебном курсе, указать связь с предыдущими темами и междисциплинарные связи; - отметить актуальность темы и ее практическое значение; - довести цель занятия; - сообщить литературные источники по теме занятия.
	Основная часть (учебные вопросы) Излагаются вопросы (проблемы), изучаемые на лекции 1. Первообразная функция и неопределенный интеграл. 2. Простейшие свойства неопределенного интеграла. Непосредственное интегрирование. 3. Замена переменной в неопределенном интеграле. 4. Интегрирование по частям
	Заключительная часть - сделать выводы по теме лекции; - ответить на вопросы студентов; - дать задание на самостоятельную работу; - объявить тему следующего занятия.

Преподаватель: _доцент Ширкунова Н.В.

(должность, подпись, инициалы, фамилия)

«22» февраля 2013 г.

Государственное образовательное учреждение

высшего профессионального образования

«Российская таможенная академия»

Кафедра таможенной статистики

УТВЕРЖДАЮ

Декан экономического

факультета

д.в.н., профессор

_________ Т.Г.Газизулин

23.02. 2013 г.

Дисциплина: Математика

Автор: к.э.н., доцент Ширкунова Н.В.

Москва

Неопределенный интеграл

Учебные вопросы:

1. Первообразная функция и неопределенный интеграл.

2. Простейшие свойства неопределенного интеграла.

3. Непосредственное интегрирование.

4. Замена переменной в неопределенном интеграле.

5. Интегрирование по частям.

Заключение

Основная литература

1. Общий курс высшей математики для экономистов. Под ред. В.И. Ермакова. – М., 2010.

2. Кремер Н.Ш. Математика для экономистов. М.:ЮНИТИ- ДАНА. 2010.

Перечень средств обучения

1. Презентации.

Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Различные вопросы математики, теории вероятности, математической статистики приводят к решению обратной задачи восстановлению функции по заданным ее производной или дифференциалу.

Определение. Функция F(x) называется первообразной для функции f(x) на данном промежутке Х, если в каждой точке этого промежутка 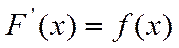или .

Для всякой непрерывной на данном промежутке функции существует первообразная.

Задача отыскания по данной функции f(x) ее первообразной решается неоднозначно, если функция F(x) – первообразная для функции f(x), то функция F(x)+C, где С – любое число, также будет первообразной.

для любого С, т.е. F(x)+C – первообразная.

Т.о., если функция f(x) имеет одну первообразную F(x), то она имеет их бесчисленное множество.

Покажем теперь, что выражение F(x)+C, где С – произвольная постоянная, исчерпывает все первообразные для функции f(x) на данном промежутке.

Теорема. Если F(x) – первообразная для функции f(x), то любая другая первообразная для f(x) (на том же промежутке) может быть записана в виде F(x)+C, где С – некоторое число.

Итак, если известна одна какая либо первообразная F(x) функции f(x) на данном промежутке, то совокупность всех ее первообразных, охватывается выражением F(x)+C, где F(x) – какая-либо первообразная, для f(x), а С – произвольная постоянная.

Определение. Совокупность всех первообразных функции f(x) на данном промежутке вида F(x)+C называется неопределенным интегралом от функции f(x) и обозначается символом .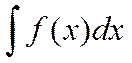

Таким образом, по определению

, где F(x) – какая-либо первообразная для f(x), а С – произвольная константа.

Функция f(x) – называется при этом подинтегральной функцией, выражение f(x)dx – подинтегральным выражением, х – переменной интегрирования, символ 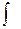- знак интеграла.

и т.д.

Определение. Отыскание первообразной и отыскание неопределенного интеграла от данной функции f(x) называется интегрированием этой функции.

Интегрирование представляет собой операцию, обратную дифференцированию.

Для того, чтобы проверить правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подинтегральную функцию.

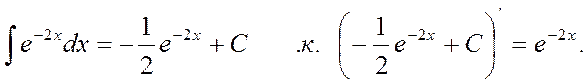
Дата добавления: 2014-01-20