
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Площадь плоской фигуры. Фигура называется плоской, если всю её, не деформируя, можно расположить на плоскости
|
|
|
|
Фигура называется плоской, если всю её, не деформируя, можно расположить на плоскости.
Площади фигур  указанных на рис. 2.1 – 2.3, вы можете найти по следующим формулам:
указанных на рис. 2.1 – 2.3, вы можете найти по следующим формулам:

| Площадь фигуры, прилегающей к оси  сверху. сверху.
| (2.1) |

| Площадь фигуры, прилегающей к оси  справа. справа.
| (2.2) |
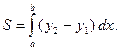
| Площадь фигуры, ограниченной линиями 
| (2.3) |
¨ Формула (2.1) была получена ранее (равенство (1.1-2). Формула (2.2) следует из формулы (2.1), если переменные  и
и  поменять ролями.
поменять ролями.




Рис. 2.1 Рис. 2.2 Рис. 2.3 Рис. 2.4
На рис. 2.3 площадь 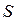 равна разности площадей под линиями
равна разности площадей под линиями  и
и 

Получилась формула (2.3). ■
З а д а ч а 1. Найдите площадь фигуры, ограниченной параболой 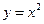 и прямой
и прямой 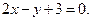
□ Составим систему уравнений  и получим
и получим 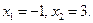
Фигура 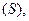 ограниченная линиями
ограниченная линиями 
 показана на рис. 2.7.
показана на рис. 2.7.
Её площадь
 ■
■
Тренировка по теме «Площадь плоской фигуры»
Найдите площадь фигур, ограниченных данными линиями.
а) 

1)  2)
2)  3)
3) 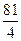 4)
4)  5)
5) 
в) 


1) 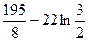 2)
2)  3)
3)  4)
4)  5)
5) 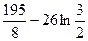
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 379; Нарушение авторских прав?; Мы поможем в написании вашей работы!