Лекция 8.1. Первообразная и неопределенный интеграл

ТЕМА 8. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

План:

1. Определение первообразной и неопределенного интеграла

2. Непосредственное интегрирование

3. Основные методы интегрирования

Из школьного курса известно, что для каждого математического действия существует ему обратное, то есть сделанные друг за другом, уничтожают результаты друг друга, а число, к которому они последовательно были применены, остается неизменным. Это вычитание и сложение, умножение и деление, возведение в степень и извлечение корня, логарифмирование – потенцированию, дифференцирование – интегрирование.

Например, если известен закон прямолинейного движения материальной точки, выражающий зависимость пути s от времени t, то скорость точки находится как производная пути по времени: 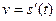. Однако может возникнуть и обратная задача: по известной скорости прямолинейного движения точки 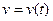, найти закон движения . Ясно, что искомая функция будет такая, для которой .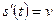

Интеграл (от лат. integer – целый), одно из самых важных понятий математики, появившееся в связи с возникшей потребностью, с одной стороны, находить функции по их производным, а с другой – находить площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т. п

Дата добавления: 2014-01-20