
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение первообразной и неопределенного интеграла
|
|
|
|
Функция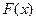 называется первообразной для функции
называется первообразной для функции 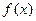 на некотором промежутке
на некотором промежутке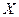 , если для любого
, если для любого 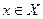 выполняется равенство:
выполняется равенство:
 .
.
Из определения ясно, что функция 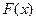 должна быть непрерывна на всем промежутке
должна быть непрерывна на всем промежутке 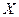 и дифференцируема во всех внутренних точках данного промежутка.
и дифференцируема во всех внутренних точках данного промежутка.
Пример. Найти первообразную для функции  .
.
Решение. Первообразной будет функция 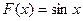 , т.к.
, т.к. 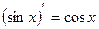 . Однако, первообразной будут и функции
. Однако, первообразной будут и функции 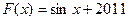 и
и  и
и 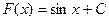 , которые отличаются только величиной слагаемого. В силу того, что производная постоянной равна нулю, имеем
, которые отличаются только величиной слагаемого. В силу того, что производная постоянной равна нулю, имеем  . Следовательно, любая функция вида
. Следовательно, любая функция вида  , где С – произвольная постоянная, будет первообразной для данной функции.
, где С – произвольная постоянная, будет первообразной для данной функции.
Возникает вопрос: исчерпывается ли множество всех первообразных для данной функции 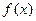 выражением вида
выражением вида  , где
, где 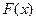 – одна из первообразных, С – произвольная постоянная.
– одна из первообразных, С – произвольная постоянная.
Теорема 7.1. (об общем виде первообразной) Две различные первообразные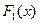 и
и  одной и той же функции
одной и той же функции 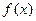 , определенной на промежутке
, определенной на промежутке 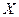 , отличаются друг от друга на постоянное слагаемое, т.е.
, отличаются друг от друга на постоянное слагаемое, т.е. 
Доказательство. Пусть функция 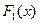 и
и  являются первообразными для функции
являются первообразными для функции 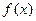 . Тогда выполняются равенства:
. Тогда выполняются равенства:  и
и 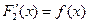 . Рассмотрим производную разности
. Рассмотрим производную разности 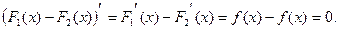 Тогда разность этих двух первообразных тождественно равна константе, т.е.
Тогда разность этих двух первообразных тождественно равна константе, т.е.  . Теорема доказана.
. Теорема доказана.
Эта теорема позволяет ввести понятие неопределенного интеграла.
Неопределенным интегралом от функции 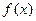 на промежутке
на промежутке 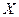 называется совокупность всех первообразных для функции
называется совокупность всех первообразных для функции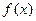 на этом промежутке и обозначается символом
на этом промежутке и обозначается символом  где
где
 знак интеграла;
знак интеграла; 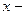 переменная интегрирования;
переменная интегрирования;
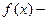 подынтегральная функция;
подынтегральная функция;  подынтегральное выражение.
подынтегральное выражение.
Процесс нахождения неопределенного интеграла называют интегрированием.
Итак, 
Возвращаясь к рассмотренному примеру, можем записать 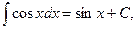 так как
так как 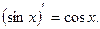
Приведем еще несколько примеров:
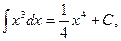 так как
так как 
 так как
так как 
 так как
так как 
С геометрической точки зрения неопределенный интеграл – это некоторое семейство кривых, определяющих одну из первообразных и отличающихся на постоянную величину.
Свойства неопределенного интеграла
Будем считать, что все рассматриваемые функции определены на промежутке 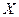 , функция
, функция 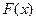 непрерывна на
непрерывна на 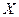 и дифференцируема во всех внутренних точках
и дифференцируема во всех внутренних точках 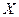 .
.
1. Производная от неопределенного интеграла равна подыитегральной функции, т.е. 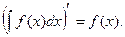
Доказательство. 
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. 
Доказательство. По определению дифференциала имеем:
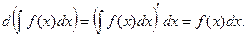
3. Интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.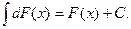
Доказательство. По определению дифференциала и определению неопределенного интеграла имеем
4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической суме интегралов от слагаемых, т.е. (для двух функций) 
Доказательство. Пусть 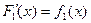 и
и 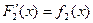 . Тогда
. Тогда

5. Постоянный множитель можно выносить за знак интеграла, т.е. для 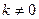 выполнено
выполнено 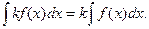
Доказательство. По свойству  имеем
имеем 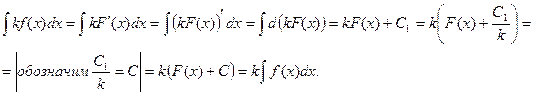
6. Если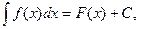 то
то 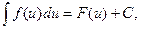 где
где  произвольная дифференцируемая функция. Это свойство называется свойство инвариантности формул интегрирования.
произвольная дифференцируемая функция. Это свойство называется свойство инвариантности формул интегрирования.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 833; Нарушение авторских прав?; Мы поможем в написании вашей работы!