
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Степени свободы
|
|
|
|
С т е п е н и с в о б о д ы – независимые геометрические параметры, полностью определяющие положение всех точек диска или системы в целом при их возможных перемещениях.
Если перемещения возникают в результате деформации материала, то для определения положения в общем случае бесконечно большого числа точек объекта (деформируемого диска) могут служить изменения (приращения) их координат при переходе из исходного положения в деформированное состояние – этих геометрических параметров, выступающих в качестве степеней свободы, получается бесконечное множество. Отсюда следует, что деформируемые системы и их элементы имеют бесконечное число степеней свободы.
Но поскольку в кинематическом анализе не ставится задача определения реальных перемещений сооружений, а, в соответствии с признаками геометрически неизменяемых, изменяемых и мгновенно изменяемых систем, требуется выявление возможности возникновения отличных от нуля (конечных или хотя бы бесконечно малых, но ненулевых) перемещений, обусловленных не деформациями, а кинематическими особенностями рассматриваемой системы, то применяется уже неоднократно упоминавшаяся выше гипотеза отвердения – предположение о недеформируемости материала всех элементов системы – как дисков, так и связей.
В результате диски рассматриваются как жёсткие, и число их степеней свободы становится конечным.
Так, несвязанный диск в пространстве имеет шесть степеней свободы: положение всех его точек однозначно определяется заданием в глобальных осях xyz (рис. 1.26) трёх координат 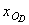 ,
, 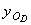 и
и 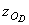 некоторой точки OD диска – начала его локальной (собственной) системы координат и трёх углов
некоторой точки OD диска – начала его локальной (собственной) системы координат и трёх углов 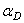 ,
, 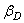 и
и 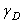 между глобальными и локальными осями.
между глобальными и локальными осями.

Рис. 1.26
В плоскости диск обладает тремя степенями свободы – это координаты  ,
,  и угол
и угол 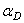 (рис. 1.27). Точка, которую можно рассматривать как диск бесконечно малых размеров (вследствие этого не требуется описывать её наклоны относительно координатных осей), в пространстве имеет три степени свободы – xA, yA и zA (рис. 1.28), а в плоскости – две (xA и yA).
(рис. 1.27). Точка, которую можно рассматривать как диск бесконечно малых размеров (вследствие этого не требуется описывать её наклоны относительно координатных осей), в пространстве имеет три степени свободы – xA, yA и zA (рис. 1.28), а в плоскости – две (xA и yA).
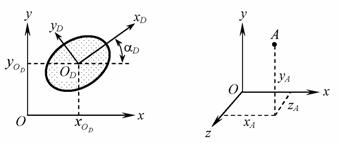
Рис. 1.27 Рис. 1.28
Роль степеней свободы также могут играть не сами вышеуказанные координаты, а их приращения по отношению к некоторому исходному значению, т.е. линейные и угловые перемещения дисков.
Каждая элементаpная cвязь отнимает однy cтепень cвободы. Каждый пpоcтой шаpниp yничтожает две cтепени cвободы взаимной подвижноcти cвязанных им диcков или блоков.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 468; Нарушение авторских прав?; Мы поможем в написании вашей работы!