Двухосное (плоское) напряженное состояние

На рисунке 31,а и 31,б приведены схемы двухосного напряженного состояния одного и того же элементарного фрагмента (размерами dx и dy) некоторого деформированного тела с произвольной ориентацией в ортогональных координатах хоу и с ориентацией в координатах главных осей 1-2.

у dx

σ_у σ₁

τ_ух σ₂

σ_х τ_ху τ_ху σ_х dy у

τ_ух σ₂ α_о

х х

σ_у σ₁

а) б)

σ_α α

τ_α σ_х

у α τ_ух τ_ху = τ_ух

х

σ_у

в)

Рисунок 31. Схемы двухосного напряженного состояния элементарного фрагмента деформированного тела: а) с произвольной ориентацией в координатах хоу;

б) с ориентацией в координатах главных осей 1-2; в) с дополнительным

косым сечением под углом α

Система обозначений компонент напряженного состояния по рисунку 31,а принята следующей: индекс х или у при нормальных напряжениях σ означает направление внешней нормали к площадке, на которой действует σ (например, напряжение σ_х действует на площадке, внешняя нормаль к которой параллельна оси х); касательные напряжения обозначаются с двойным индексом: первый из них совпадает с индексом при нормальном напряжении, действующем на этой же площадке, второй – параллельно какой оси направлено это касательное напряжение (например, напряжение τ_ху действует на площадке, внешняя нормаль к которой параллельна оси х, направление τ_ху параллельно оси у). У нормального напряжения оба индекса совпадают, поэтому применяется только один индекс.

При двухосном напряженном состоянии деформированного тела, рассматриваемом в ортогональной двухосной системе координат получают, как отмечалось выше, два главных напряжения, а оси 1 и 2, параллельно которым направлены 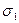и 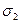, взаимно перпендикулярны.

При известных (заданных) в некоторой системе координат хоу значениях компонент напряженного состояния σ_х, σ_у, τ_ху = τ_ух (по закону парности касательных напряжений) всегда можно определить единственно возможный угол ориентации α_о положения главных площадок, а, следовательно, и главных осей 1 и 2 действия главных напряжений σ₁ и σ₂.

Рассечем элементарный фрагмент деформированного тела дополнительны косым сечением под произвольным (положительным) углом α, отложенным против хода часовой стрелки от оси х, см. рисунок 31,в и рассмотрим его равновесие. При этом примем, что σ_у > σ_х. Площадь наклонной грани обозначим dA, тогда площадь вертикальной грани будет равна dA·sinα и горизонтальной грани dA·cosα. Помня, что сила равна произведению напряжения на площадь, составляем уравнения равновесия проекций всех сил:

- на ось, совпадающую с направлением нормального напряжения σ_α,

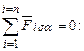
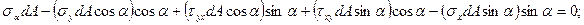
- на ось, совпадающую с направлением касательного напряжения τ_α,

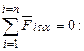
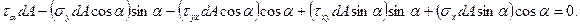
После сокращения на dA, ввода тригонометрических функций двойных углов, учитывая равенство значений τ_ху = τ_ух, получим выражения напряжений на наклонной площадке:

(31)

(32)

Очевидно, что изменение угла наклона α наклонной площадки приводит к изменению значений напряжений σ_α и τ_α. Для определения положения (угла наклона α = α_о, см. рисунок 31,б) главных площадок, на которых касательные напряжения равны нулю, а нормальные напряжения имеют экстремальные значения, можно либо приравнять нулю производную 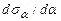, либо приравнять нулю касательные напряжения . В обоих вариантах после

элементарных преобразований получаем формулу для расчета угла α_о наклона главных площадок площадкам, попарно параллельным к осям х и у:

или 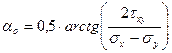. (33)

Анализируя вторую производную , можно установить, что на главной площадке под углом 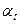(при принятом выше условии ) действует первое (максимальное) главное напряжение , а на площадке под углом действует второе (минимальное) главное напряжение . Можно получить также формулы для практических расчетов одиночных углов и наклона соответственно главных осей 1 и 2 к оси х (см. ([1], с. 349):

; . (34)

Чтобы вывести формулу для расчета экстремальных значений нормальных напряжений (главных напряжений σ_max= σ₁ и σ_min= σ₂) надо вначале полученное выше выражение для tg2α_o подставить в ранее полученную формулу для определения σ_α. Затем, используя известные выражения тригонометрических функций двойных углов, после преобразований можно получить следующие формулы для расчетов двух главных напряжений:

; (35)

. (36)

Если одно из заданных напряжений (σ_х или σ_у) равно нулю, а другое равно σ, то формулы для расчета главных напряжений будут более простыми:

; (37)

. (38)

Последние две формулы применяются при расчетах элементов конструкций на изгиб и сложное сопротивление (эти темы рассматриваются в соответствующих разделах курсов «Инженерная механика 1 и 2»).

Приравнивая нулю производную выражения 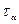(т. е. ), можно получить формулы для расчета экстремальных значений касательных напряжений:

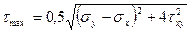; . (39)

Максимальное касательное напряжение можно получить также как полуразность главных напряжений:

. (40)

Следует помнить, что в вышеприведенных формулах все компоненты напряженного состояния следует подставлять с их алгебраическими знаками. Растягивающие нормальные напряжения σ общепринято считать положительными, а сжимающие – отрицательными.

Знаки касательных напряжений τ зависят от направлений осей координат и внешних нормалей к площадкам, где они действуют. Внешняя нормаль – это воображаемая прямая, перпендикулярная к рассматриваемой площадке, направленная от фрагмента анализируемого напряженно-деформируемого тела. Если внешняя нормаль данной площадки совпадает с направлением соответствующей оси координат, то на этой площадке напряжение τ положительно при совпадении его направления с соответствующей осью; если же внешняя нормаль к данной площадке противоположна направлению координатной оси, то напряжение τ положительно в тех случаях, если оно также противоположно своей координатной оси. В частности, все компоненты напряжений, изображенные на рисунке 31,а в координатах хоу, положительны.

Дата добавления: 2014-01-11