Задачи теории конечных автоматов

Realisation of Adjectival Categories

The form-derivation system of English adjectives, i. e. their paradigm, is very poor, it is even poorer than that of nouns. In the history of the English language development the morphology of English adjectives underwent great changes which were caused by the crucial changes in all the classes of nouns. The reduction of the paradigm led to the obliteration of case, number and gender distinctions in the forms of English adjectives. As a result, it is only the category of Degree that is realized in the form-derivation of adjectives.

The category of Degree of English adjectives is restricted in its realization by the implicit meaning of Qualitativeness/Non-Qualitativeness inherent in adjectives, the latter being classed accordingly into qualitative and non-quali­tative adjectives. Only qualitative adjectives, due to their meaning, are associated with Graduality. The quality de­noted by such adjectives is conceived as being gradual. That is why qualitative adjectives in English are inflected for De­gree. The paradigm of adjectives in Modern English is very much reduced and consists of the three categorial forms through which the category of Degree is realized.

The com­parative and the superlative degree categorial forms can be marked synthetically by the inflections as in longer, longest; easier, easiest and by suppletivity as in bet­ter, best; less, least. The question whether the degree catego­rial forms of English adjectives can or cannot be derived analytically remains open because the combinations like more interesting or most doubtful are not unanimously recognized as analytical adjectival forms. Some scholars are inclined to treat them as lexico-syntactical devices of expressing the conceptual category of Graduality. Such a view is probably justified because, by strict definition, analytical markers are binary units consisting of the auxiliary element and, what is extremely important, of the particular unchangeable form of the notional word as in: Vbe + Ving (the Continuous markers), Vhave + Ven (the Perfect marker). So far as the above combinations like more interesting or most doubtful are concerned, they do not satisfy the requirements for analy­tical formations. They are likely to be lexico-syntactical combinations of words.

В процессе логического проектирования асинхронных конечных автоматов можно выделить две задачи синтеза и две задачи анализа.

1. Абстрактный синтез.

На первом этапе абстрактного синтеза по словесному описанию алгоритма работы автомата строится первичная таблица переходов (или граф-схема). Как правило, первичная таблица переходов бывает избыточной, поскольку она содержит одно устойчивое состояние в каждой строке.

На втором этапе абстрактного синтеза проводится минимизация числа внутренних состояний (минимизация таблицы переходов).

2. Абстрактный анализ.

При решении задачи анализа по таблице переходов требуется получить словесное описание алгоритма функционирования КА.

3. Структурный синтез заключается в выборе элементарных автоматов (ЭА) и отыскании такого способа их соединения между собой, который обеспечивает функционирование схемы в соответствии с заданной кодированной таблицей переходов и выходов. Кодированная таблица переходов определяет зависимость внутренних состояний и выходных сигналов КА от значений входных сигналов и внутренних состояний в предыдущий момент времени (такт). Кодирование внутренних состояний осуществляется таким образом, чтобы исключить критические состязания.

Для синтеза КА необходимо иметь функционально полный набор элементов, который должен содержать:

– хотя бы один ЭА с двумя разными состояниями, для которого соблюдается условие полноты системы переходов и выходов (то есть существует хотя бы один входной сигнал, переводящий автомат из состояния 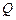в 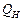и в каждом состоянии автомат выдаёт выходной сигнал, отличный от сигналов, выдаваемых в других состояниях);

– логические элементы, образующие функционально полную систему для синтеза логических функций.

4. Структурный анализ.

При решении задачи структурного анализа по схеме автомата необходимо получить таблицу переходов и сравнить с исходной таблицей с целью проверки правильности синтеза.

МИНИМИЗАЦИЯ ТАБЛИЦ ПЕРЕХОДОВ

При построении первичной таблицы переходов, как правило, определяются некоторые устойчивые состояния, которые соответствуют определённым комбинациям входных сигналов (столбцам таблицы) и обеспечивают реализацию заданного алгоритма функционирования КА. Начиная с этих устойчивых состояний, как с некоторого базиса, находятся переходы между ними и заполняются соответствующие клетки таблицы переходов. При этом может случиться, что выбранных устойчивых состояний недостаточно для исчерпывающего описания алгоритма функционирования проектируемого автомата. В этом случае необходимо добавить ещё некоторые новые устойчивые состояния. Не будет особого ущерба, если использовано слишком много состояний. Дело в том, что следующим этапом процедуры синтеза является нахождение таблицы переходов с минимальным числом состояний, которая удовлетворяет требованиям, заложенным в исходную первичную таблицу переходов.

Два автомата называются эквивалентными, если на одинаковую входную последовательность они выдают одинаковые выходные сигналы. Задача минимизации сводится к нахождению такого эквивалентного заданному автомата, который имеет минимальное число состояний памяти. Методы проведения минимизации изложены в [1].

МЕТОД АНГЕРА-ПОЛА МИНИМИЗАЦИИ ТАБЛИЦ ПЕРЕХОДОВ АСИНХРОННЫХ КОНЕЧНЫХ АВТОМАТОВ

В процессе минимизации необходимо найти совместимые состояния автомата, то есть такие состояния, которые покрываются одной и той же строкой минимизированной таблицы переходов. Очевидно, что необходимым условием совместимости двух состояний АП (строк таблицы переходов) является совместимость выходных сигналов в тех столбцах, где они определены (совместимость по выходам).

Поиск совместимых строк удобно производить с помощью специальной треугольной таблицы, в которой отмечаются условия совместимости и эквивалентности строк. Рассмотрим построение такой таблицы на примере автомата, заданного табл. 10.

Таблица 10

	(0),0			*
	*	*	(1),1
		(2),0	*
		*	(3),1
	(4),1			*
	*			(5),0
		*	(6),0
				(7),1

Строки треугольной таблицы совместимости (таблицы Ангера-Пола, табл. 11) обозначаются состояниями автомата кроме нулевого, а столбцы состояниями кроме последнего. В клетки указанной таблицы вносятся следующие обозначения:

– состояния неэквивалентны (несовместимы).

– состояния безусловно совместимы.

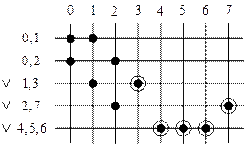
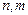– строки совместимы при условии совместимости указанных строк (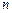и ).

Таблица 11

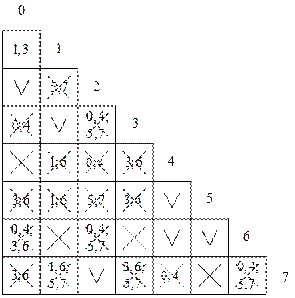
После заполнения таблицы вычёркиваем те клетки, для которых условие совместимости пар не выполняется (пунктирные линии в табл. 11). Например, строки 0 и 4 несовместимы, следовательно, не будут совместимы и строки (2, 4), (4, 7), (6, 7) и т. д.

Из таблицы Ангера-Пола можно выписать достаточно большое количество групп совместимых строк. Задача сводится к определению минимального количества групп, необходимого для покрытия исходной таблицы переходов. Это удобно делать с помощью таблицы покрытий Квайна-Мак-Класски (табл. 12). По столбцам располагаем исходные состояния автомата, по строкам – максимально – совместимые группы состояний (строк).

На пересечении строк и столбцов точками отмечаем те состояния, которые входят в максимально совместимые группы. Далее кружком отмечаем те состояния, которые покрываются всего один раз (то есть одна точка в столбце). Остальные состояния необходимо покрыть минимальным количеством групп.

Таблица 12

Кодируем новые состояния автомата (табл. 13).

Таблица 13

Группа (строка)	Код
(0, 1)
(1, 3)
(2, 7)
(4,5,6)

Далее строим минимизированную таблицу переходов (табл. 14).

Таблица 14

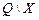
	(0),0
		*	(1),1
		(2),0		(2),1
	(3),1		(3),0	(3),0

В общем случае, при большом числе входных сигналов и не полностью заполненных таблицах переходов (то есть используются не все комбинации входных переменных), возможна минимизация количества столбцов. При этом на входе автомата выделяется комбинационная схема, осуществляющая перекодирование входных сигналов в управляющие сигналы автомата. Для осуществления такой операции количество различных столбцов должно быть как минимум в два раза меньше общего количества столбцов таблицы переходов.

Рассмотрим ещё один пример минимизации таблицы переходов КА, заданного табл. 15.

Таблица 15

	(0),0
			(1),0
				(2),1
		(3),0
			(4),0
				(5),0
		(6),0
				(7),1

Строим таблицу Ангера-Пола (табл. 16).

Таблица 16

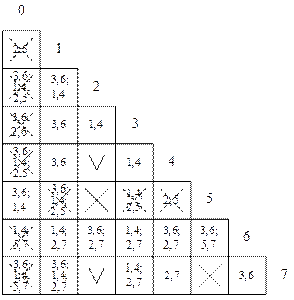
Кодируем группы совместимых строк (табл. 17)

Таблица 17

Группа (строка)	Код
(0, 5)
(1, 2, 3, 4, 5, 6, 7)

Минимизированная таблица переходов (табл. 18).

Таблица 18

	(0),0			(0),0
		(1),0	(1),0	(1),1

Дата добавления: 2014-01-11