Метод мацевитного-денисенко

Противогоночное кодирование может заключаться в развязывании тех пар состояний, для которых осуществляется переход под действием одного и того же сигнала. Пусть 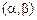и 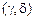– две пары двоичных кодов. Пары 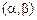и 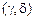называются развязанными, если некоторый разряд кода принимает одно значение на паре 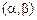и противоположное на паре .

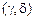Л. В. Мацевитный и Е. Л. Денисенко доказали следующую теорему:

В автомате, состояния которого закодированы двоичными кодами конечной длины (КА), гонки отсутствуют тогда и только тогда, когда для двух любых переходов 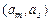и 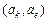, , происходящих под действием одного и того же входного сигнала, пары кодов состояний развязаны.

Суть этого метода заключается в том, что развязывая коды состояний, мы исключаем критические состязания.

В качестве примера рассмотрим кодирование состояний счетчика-делителя частоты на 3, функционирование которого задано таблицей переходов 6.

Указанная таблица содержит переходы, при которых меняются несколько внутренних переменных. Следовательно, для обеспечения правильной работы рассматриваемого автомата необходимо осуществить противогоночное кодирование путём развязывания пар переходов, осуществляемых под действием одинаковых сигналов:

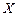– переход входного сигнала из состояния 0 в состояние 1 и

– переход входного сигнала из состояния 1 в состояние 0.

Переходы, которые осуществляются в рассматриваемой таблице под действием сигналов 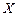и приведены в табл. 26.

Таблица 26

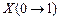
(0, 1)	(0, 0)
(1, 1)	(1, 2)
(2, 3)	(2, 2)
(3, 3)	(3, 4)
(4, 5)	(4, 4)
(5, 5)	(5, 0)

Построим таблицу кодов состояний синтезируемого автомата (табл. 27), которая должна содержать шесть строк – 0, 1, 2, 3, 4, 5 (по количеству внутренних состояний) и три столбца – , , 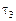(по количеству двоичных разрядов, необходимых для кодирования состояний).

Таблица 27

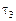
Пару переходов (0,1) и (1,1) развязывать нет необходимости, поскольку в обоих случаях автомат переходит в состояние 1.

Для развязывания пары переходов (0, 1) и (2, 3) необходимо разряду кода присвоить значение 0 для группы (0, 1) и значение 1 – для группы (2, 3).

Для развязывания пары переходов (0, 1) и (3, 3) необходимо разряду кода присвоить значение 1 для состояния 3, входящего в группу (3, 3).

Аналогично, для развязывания пары переходов (0, 1) и (4, 5) необходимо разряду кода присвоить значение 1 для состояний 4 и 5, входящих в группу (4, 5).

Пара переходов (0, 1) и (5, 5) уже развязана по переменной .

Далее рассматриваются все пары переходов, начиная с группы (1, 1). Все указанные переходы уже развязаны по переменной .

Для развязывания пар переходов (2, 3) и (4, 5) необходимо использовать разряд кода , поскольку в разряде указанные состояния имеют одинаковые (нулевые) значения.

Аналогичным образом рассматриваются все возможные пары переходов, происходящие под действием одних и тех же входных сигналов. В случае необходимости (если не удаётся развязать все имеющиеся пары переходов) вводятся дополнительные разряды кодов состояний.

Сопоставляем полученные трёхразрядные коды состояниям автомата и строим новую (перекодированную) таблицу переходов (табл. 28).

Таблица 28

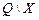
	4,1	(0),1
	*	*
	(2),0	0,*
	*	*
	(4),1
	7,*	(5),1
	2,0	(6),0
	(7),0	6,0

Все переходы синтезированного автомата являются соседними:

2 – 0 – 4 – 5 – 7 – 6 – 2 … и т. д.

Можно построить таблицу переходов с нулевым устойчивым начальным состоянием (табл. 29).

Таблица 29

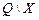
	(0),0	4,*
	*	*
	0,0	(2),0
	*	*
		(4),1
	(5),1
	(6),0	2,0
	6,*	(7),1

Дата добавления: 2014-01-11