Свойства разбиений

Говорят, что разбиение Р мельче чем разбиение 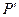(или 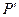крупнее Р), (или Р следует за 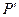) и записывают , если все точки разбиения 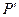содержатся среди точек разбиения Р. Отметим три важных свойства отношения «крупнее – мельче» для разбиений:

а) существуют разбиения со сколь угодным малым параметром:

I = [ a, b ]. Выбирая ; k = 0,1,2,…, n. Тогда и выбирая достаточно большим, можно сделать параметр разбиения сколь угодно малым.

б) для двух любых разбиений существует третье разбиение, следующее за любым из них:

с) транзитивность отношения «крупнее – мельче»:

и, что то же самое P ₁ É P ₂ Ù P ₂ É P ₃ Þ P ₁ É P ₃.

Дата добавления: 2014-01-11