Воспоминания о будущем

Пусть V_n – линейное пространство.

Def.: В множестве R введено скалярное произведение, если 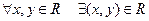такое, что: ; ;

; .

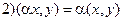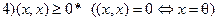Если в линейном пространстве V_n введено скалярное произведение, то пространство называется евклидовым пространством (в дальнейшем евклидово пространство, зачастую, будет обозначаться .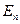

Def.: В множестве R введена норма, если , такое, что:

; ; .

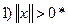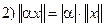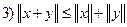Линейное пространство V_n, в котором введена норма называется нормированным пространством.

Def. В множестве R введена метрика, если 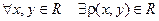такое, что

; ; .

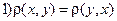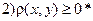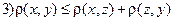Если в множестве R введена метрика, то R называется метрическим пространством.

Если в пространстве V_n введено скалярное произведение (V_n –евклидово пространство E_n), то в нем можно естественным образом ввести норму 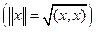и метрику .

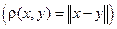Говорят что, норма и метрика индуцируются скалярным произведением.

Пусть E_n – евклидово пространство с индуцированными нормой и метрикой, и – ортонормированный базис в E_n.

Тогда: .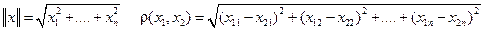

Def: открытый шар.

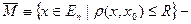замкнутый шар.

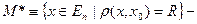сфера

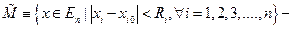открытый параллелепипед

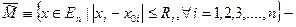замкнутый параллелепипед.

Def: 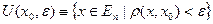– ε - окрестность точки х ₀.

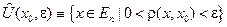– проколотая ε - окрестности точки х ₀.

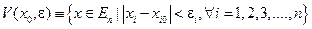– прямоугольная окрестность точки х _0.

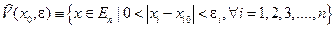проколотая прямоугольная ε - окрестность.

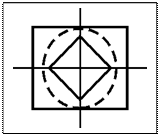F°. Любая ε – окрестность точки содержится в некоторой прямоугольной окрестности той же точки и, наоборот, содержит в себе некоторую прямоугольную окрестность той же точки.

Факт этот свидетельствует о том что, топологии введенные с помощью прямоугольных и сферических окрестностей эквивалентны.

Аксиома полуотделимости: Из любых двух точек евклидового пространства каждая имеет окрестность, не содержащая другую точку.

Аксиома отделимости: Д ля любой пары точек евклидового пространства существуют их непересекающиеся окрестности.

Def: Точка Р (х ₁, …., х_n) называется внутренней точкой множества М, если .

Def: Точка Р называется граничной точкой множества М, если

.

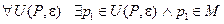
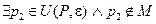Def: Точка Р называется предельной точкой множества М (или точкой сгущения), если

.

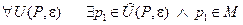Def: Множество М называется открытым, если все его точки внутренние.

Def: Множество М называется ограниченным, если .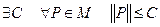

Def: Если 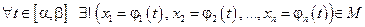, то говорят, что в множестве М задана кривая. Кривая L: 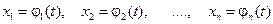называется непрерывной, если 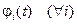- непрерывные функции.

Def: Множество М называется связным, если любые его точки можно соединить непрерывной кривой, все точки которой принадлежат множеству М.

Def: Множество М называется односвязным, если любой замкнутый контур в множестве М можно непрерывным движением стянуть в точку принадлежащую множеству М.

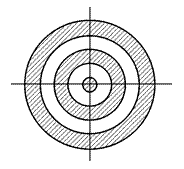
Пример: область определения функции 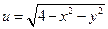– круг радиуса 2 с центром в начале координат – связна, а область определения функции 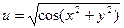– концентрические кольца (см. рис.) –не связна:

.

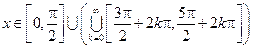Def: Последовательность 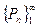точек евклидового пространства называется сходящейся, к элементу пространства Р , если .

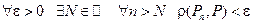Тº. Для того, чтобы 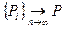необходимо и достаточно, чтобы последовательности координат сходились к соответствующей координате т. Р.

Δ 1) Пусть 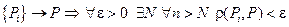, т.е.

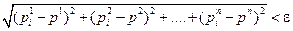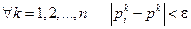Þ Þ .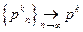

2) Пусть последовательность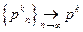, тогда 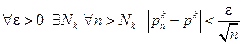, и значит 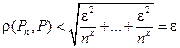Þ ▲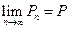

Def: Последовательность 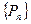точек евклидового пространства называется фундаментальной, если .

Тº. Для того, чтобы последовательность сходилась необходимо и достаточно, чтобы она была фундаментальной.

Δ. Доказательство основано на переходе к покоординатной сходимости и ссылке на то, что для числовых последовательностей этот факт доказан. ▲

Тº. (Больцано - Вейерштрасса) Из любой бесконечной ограниченной последовательности точек евклидового пространства можно выделить сходящуюся подпоследовательность.

Δ Задана бесконечная, ограниченная последовательность 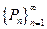, такая, что 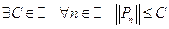. Рассмотрим последовательность первых координат элементов

этой последовательности 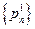. Это бесконечная и ограниченная числовая последовательность и, следовательно, из нее можно выделить сходящуюся подпоследовательность . Тем самым, из последовательности 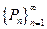выделена подпоследовательность 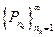, у которой последовательность первых координат сходится. Обозначим элементы этой последовательности вновь .

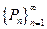Далее рассмотрим последовательность вторых координат элементов этой последовательности , и проведем ту же процедуру. … Проделав эту процедуру m раз (m – размерность евклидового пространства), в конце концов, получим последовательность 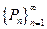с покоординатной сходимостью. Следовательно, построенная последовательность сходится. ▲

Дата добавления: 2014-01-11