Различные виды уравнения плоскости

1.Уравнение плоскости, проходящей через данную точку М₀(x₀,у₀,z₀) перпендикулярно вектору n(А,В,С):

A(x-x₀)+B(y-y₀)+C(z-z₀)=0 (1.3.1)

Пример 1.3.1. Записать уравнение плоскости, проходящей через точку M₀ (1, 2, 3), перпендикулярно вектору n(2,-1,4). Используя уравнение (1.3.1), получим 2(x-l)-l(y-2)+4(z-3)=0 или 2x-y+4z-l2-0.

Пример 1. 3. 2.Составить уравнение плоскости, проходящей через точку М₀ (1,2,3) пареллельно векторам a (3,-1.,0) и b (2,l,2).

Плоскость пареллельна векторам а и b, поэтому вектор нормали к плоскости n(А,В,С) равен векторному произведению векторов)

а и b и находится по формуле (1.2.10):

Уравнение искомой плоскости (1.3.1) имеет вид

-2(x-l)-6(y-2)+5(z-3)=0 или -2x-6y+5z-l=0.

2.Общее уравнение плоскости:

Ax+By+Cz+D=0 (1.3.2)

В этом уравнении коэффициенты А, В,С -координаты вектора п(А,В,С) перпендикулярного плоскости.

3.Уравнение плоскости в отрезках

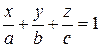
Числа a,b,c равны величинам направленных отрезков, отсекаемых на осях координат.

4.Уравнение плоскости, проходящей через три точки M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂), М₃(x_3, у₃, z₃), не лежащие на одной прямой

Пример 1.3.3.Составить уравнение плоскости, проходящей через три точки M₁(1,2,3), M₂(-1,1,1), М₃(0,2,1).

В соответствии с уравнением (1.3.4) получаем

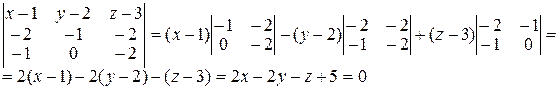
т.е. 2x-2y-z+5=0

и есть уравнение искомой плоскости.

Дата добавления: 2014-01-11