Различные видах уравнений прямой в пространстве

1.Общее уравнение прямой A₁x+B₁y+C₁z+D₁=0

A₂x+B₂y+C₂z+D₂=0 (1.3.5)

Прямая задана пересечением двух плоскостей с нормалями n₁(A₁, B₁, C₁) и

n₂ (A₂, B₂, C₂)

2.Канонические (стандартные) уравнения прямой, проходящей через точку

М₀ (x₀, y₀, z₀) и имеющей направляющий вектор а(т,п,р)

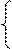
Пример 1.3.4.Перейти от общих уравнений прямой

2x+3y-z+2=0

x-y-3z+6=0 к каноническим уравнениям. Прежде всего выберем какую-

нибудь точку М₀, например М₀ (0,0,2), удовлетворяющую общим уравнениям прямой. Если сразу не удается подобрать координаты точки М₀, то эту точку можно найти из решения системы линейных уравнений (см. пример 1.1.11), которой задаются общие уравнения прямой.

Направляющий вектор прямой а может быть выбран в виде a=n₁xn₂ (см. 1.3.5), где n₁ (2,3,-l) и n₂ (1,-1,-3) -нормальные векторы к плоскостям, пересечением которых и задается прямая

'Канонические уравнения прямой имеют вид

3. Параметрические уравнения прямой

x = x₀ + mt, y = y₀ + pt, z = z₀ + ut, t є R (1.3.7)

Пример 1.3.5.В примере 1.3.4 от канонических уравнений прямой перейти к параметрическим уравнениям.

Ряд равных отношений в канонических уравнениях прямой примера 1.3.4 приравняем к t:

Откуда получим параметрическиe

уравнения x=-t, y=t, z=2-t, t є R.

4.Уравнение прямой, проходящей через две точки M₁(x₁, y₁, z₁), М₂(х₂, у₂, z₂).

Замечание. В уравнениях прямой (1.3.6) и (1.3.8) допускаете равенство нулю одной или двух координат вектора а(т,п,р). В этом случае нуль в знаменателе воспринимается только лишь как информация о координатах вектора а.

Дата добавления: 2014-01-11