Модель финансовой деятельности фирмы

3.1. Содержательное описание финансовой деятельности фирмы

Разрабатывается план строительства нового предприятия, которое будет выпускать определенную продукцию, пользующуюся спросом на рынке. Аналогичную продукцию выпускают и некоторые другие фирмы, поэтому придется действовать в условиях конкуренции.

Изначально можно приближенно оценить предполагаемые эксплуатационные расходы по выпуску продукции, т. е. можно считать известными математическое ожидание (среднее значение) расходов и среднее квадратическое отклонение этих расходов. С математической точки зрения это значит, что можно принять допущение о нормальном распределении расходов с заданными параметрами.

Относительно возможностей сбыта продукции и характеристик рынка можно предположить, что емкость рынка также имеет нормальное распределение с некоторыми известными параметрами: математическим ожиданием и средним квадратическим отклонением. Хуже обстоит дело с определением характеристик той доли в рынке, которую может завоевать предприятие после его вступления в строй. Единственно, что можно здесь предсказать, - это средняя величина этой доли. Вид распределения неизвестен, и нет основания для того, чтобы считать его нормальным. В этом случае при создании модели исследуемого процесса можно использовать распределение произвольного типа, например кусочно-равномерное. Можно выбрать несколько вариантов такого распределения и проанализировать реакцию модели на изменение его параметров.

В качестве показателя эффективности логично будет выбрать минимальную гарантированную прибыль от продажи продукции. При этом предполагается, что случайная величина прибыли имеет нормальное распределение.

3.2. Концептуальная модель

Пусть намечается строительство нового предприятия при следующих условиях

1. Выпуск продукции связан с эксплуатационными расходами, которые имеют нормальное распределение с заданными параметрами: математическим ожиданием расхода Mrash и средним квадратическим отклонением расхода .

2. Емкость рынка, где должна реализовываться продукция предприятия, имеет нормальное распределение с заданными параметрами: математическим ожиданием емкости рынка М_run и средним квадратическим отклонением емкости рынка .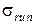

3. Доля предприятия в рынке является неопределенной и может быть задана некоторой произвольной функцией распределения (например, кусочно-равномерной функцией).

4. Случайная прибыль предприятия определяется по следующей зависимости:

Prof= Ryn • Dol - Rash,

где Ryn - случайная величина емкости рынка; Dol - случайная величина доли предприятия на рынке; Rash - случайная величина эксплуатационных расходов предприятия.

Выходными характеристиками модели являются: сумма случайных величин прибыли для Np случайных реализаций

• сумма квадратов случайных величин прибыли для Np случайных реализаций.

Показателем эффективности работы предприятия является минимальная гарантированная прибыль, определяемая по следующим зависимостям:

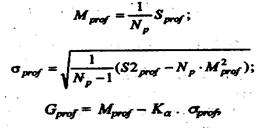
где Mprof - математическое ожидание (среднее значение) прибыли; бprof -среднее квадратнческое отклонение прибыли; Кa - квантиль нормального распределения, соответствующий заданной надежности a (Ka = 1,28 при а = 0,9); Gprof - минимальная гарантированная прибыль.

3.3. Алгоритм модели

В макет стартовой формы включены следующие объекты управления: несколько меток с заголовками объектов, двенадцать текстовых полей для корректировки исходных данных, три текстовых поля для вывода результатов моделирования и три командные кнопки для управления работой программы.

Схема алгоритма процедур обработки прерываний показана на рис. 19.7.

После нажатия кнопки «Start» активизируется стартовая форма. С этого момента программа находится в режиме ожидания действий пользователя.

Рис. 19.7. Схема алгоритма процедур обработки прерываний

Цифрой 2 обозначено действие, заключающееся в нажатии (с помощью мыши) кнопки «Расчет». В процедуре, связанной с этой кнопкой, оператор 3 осуществляет перевод исходных данных из символьной формы в числовую. Затем оператор 4 обращается к модулю общего назначения «Model 6». Схема алгоритма этого модуля приведена на рис. 19.8. После окончания работы модуля и выдачи на экран результатов моделирования работа процедуры, связанной с кнопкой «Расчет», заканчивается. Программа вновь переходит в режим ожидания действий пользователя.

Цифрой 5 на схеме обозначено действие пользователя, заключающееся в нажатии кнопки «Очистка». В процедуре, связанной с ней, производится очищение текстовых полей для вывода выходных характеристик модели. Затем может быть произведено изменение исходных данных и проведены новые расчеты с использованием кнопки «Расчет».

Цифрой 7 на схеме обозначено действие пользователя, заключающееся в нажатии кнопки «Выход». В результате работа программы прекращается.

Рнс. 19 8.Схема алгоритма модуля «Model 6»

Оператор 1 производит обнуление глобальных переменных, к которым относятся:

• сумма прибылей для всех случайных реализаций;

• сумма квадратов прибылей для всех случайных реализаций. Оператор 2 является началом цикла случайных реализаций» Оператор 3 обращается к процедуре, вырабатывающей возможные значения нормированных и центрированных случайных величин с нормальным распределением. Оператор 4 определяет случайное значение эксплуатационных расходов.

Операторы 5 и 6 аналогичным образом определяют случайную величину емкости рынка.

Оператор 7 обращается к процедуре, которая определяет возможное значение случайной доли предприятия в рынке. Оператор 8 определяет величину случайной прибыли для одной реализации моделируемого процесса. В операторе 9 происходит накопление сумм прибылей и сумм квадратов прибылей для всех случайных реализаций.

После окончания цикла случайных реализаций оператор 10 определяет показатель эффективности по формуле

Gprof = Mprof - K_a

Оператор 11 выводит результаты моделирования на экран.

Случайная доля предприятия в рынке согласно принятому допущению имеет кусочно-равномерное распределение в выбранном диапазоне. Схема алгоритма процедуры, генерирующей возможные значения случайной величины с таким распределением, показана на рис. 19.9.

Оператор 1 обращается к стандартной процедуре генерирования случайной величины с равномерным распределением в интервале (0,1).

Оператор 2 является заголовком цикла, в котором поочередно рассматриваются все участки выбранного диапазона. Заметим, что число участков на единицу меньше числа граничных точек.

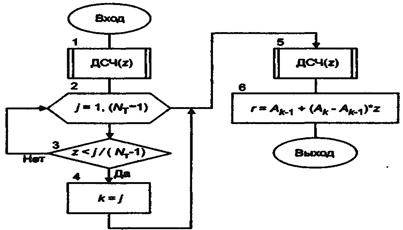
Рис. 19.9, Схема алгоритма процедуры генерирования случайных величин с кусочно-равномерным распределением

Оператор 3 проверяет условие попадания в j-и участок, а оператор 4 фиксирует номер участка.

Оператор 5 вновь обращается к генератору случайных чисел с равномерным распределением в интервале (0,1).

Оператор 6 определяет значение случайной переменной r по формуле

r = A_k-1 + z(a_k-a_k-1).

3.4. Пример решения задачи моделирования

Примем следующие исходные данные:

• среднее значение эксплуатационных расходов Мrash =$110 000;

• среднее квадратическое отклонение эксплуатационных расходов 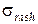=$11000;

• среднее значение емкости рынка Мryn =$2 750 000;

• среднее квадратическое отклонение емкости рынка 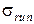=$250 000;

• число случайных реализаций Np - 10 000.

Варьируемыми переменными будем считать параметры кусочно-равномерного распределения доли предприятия в рынке. Рассмотрим три варианта распределения.

Для первого варианта примем, что число граничных точек N_T=2 (диапазон состоит из одного участка). Пусть среднее значение доли равно 0,1. Граничные точки расположим симметрично относительно среднего значения. Выберем следующие значения их координат:

А₀ = 0,099 и А₁ = 0,101.

Таким образом, для первого варианта степень неопределенности достаточно мала, доля предприятия в рынке практически постоянна и составляет 10% общей емкости рынка.

Для второго варианта примем, что число граничных точек N_T =6 (диапазон состоит из пяти участков). Пусть среднее значение случайной переменной по-прежнему равно 0,1. Граничные точки расположим симметрично относительно среднего значения. Выберем следующие значения их координат:

Aо=0,035; A₁₌ 0,075; А₂ =0,095; А₃ =0,105; А₄ = 0,125; А₅ = 0,165.

Плотности распределения вероятностей определяются из условия, что вероятности попадания на любой из участков должны быть одинаковы и равны величине 1/ (NT- 1). Вид полученного распределения показан на рис. 19.10.

Таким образом, для второго варианта доля предприятия в рынке характеризуется достаточной степенью неопределенности. Случайная величина этой доли неравномерно распределена в диапазоне от 0,035 до 0,165.

Рис. 19.10. Кусочно-равномерное распределение доля в рынке (второй вариант)

Для третьего варианта примем, что число граничных точек nt также равно шести (диапазон состоит из пяти участков). Пусть среднее значение случайной переменной по-прежнему равно 0,1. Граничные точки расположим несимметрично относительно значения Dol = 0,1. Выберем следующие значения их координат:

Aо=0,035; A₁ = 0,075; А₂ = 0,095; А₃ = 0,105; А₄ = 0,155; А₅ = 0,255.

Так же, как и для других вариантов, условие, которому должно удовлетворять кусочно-равномерное распределение, состоит в том, что вероятности попадания на любой из участков должны быть одинаковы и равны величине 1/ (NT-1). Вид полученного распределения показан на рис. 19.11.

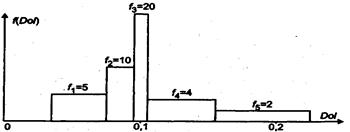
Рис.19.1. Кусочно-равномерное распределение – доля в рынке (вар.3)

Таким образом, для третьего варианта доля предприятия в рынке характеризуется еще большей неопределенностью. Случайная величина этой доли неравномерно распределена в диапазоне от 0,035 до 0,255.

Варианты исходных данных, относящиеся к описанию кусочно-равномерных распределений доли предприятия в рынке, сведены в табл. 19.2.

Таблица 19.2 Параметры кусочно-равномерных распределений

^№ Число Координаты точек (границ участков)

вари-

анта точек

1 2 3 4 5 6

1 2 0,099 0,101 - - - -

2 6 0,035 0,075 0,095 0,105 0,125 0,165

3 6 0,035 0,075 0,095 0,105 0,155 0,255

Результаты моделирования отражены в табл. 19.3

Таблица 19.3 Результаты моделирования

№ варианта Mprof,,$ , $ Gprof, $ 1 164,6 27,2 129,8 2 165,2 90,8 49,0 3 205,1 150,9 11,9

Анализ приведенных данных показывает, что с увеличением степени неопределенности при описании доли предприятия в рынке средняя прибыль растет, однако минимальная гарантированная прибыль уменьшается из-за увеличения разброса случайной величины прибыли.

Дата добавления: 2014-01-11