Сумма простых дробей приводится к общему знаменателю и числитель получившейся дроби приравнивается к числителю исходной дроби

или

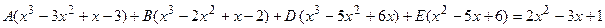
или после раскрытия скобок и приведения подобных членов получаем

6. Сравнивая коэффициенты при одинаковых степенях переменной величины в левой и правой частях равенства, получают систему линейных алгебраических уравнений (СЛАУ) относительно неизвестных коэффициентов :

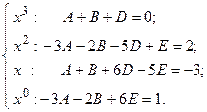
З5. Если разложение полинома, стоящего в знаменателе дроби, на простые множители содержит не кратные действительные корни, то процедура отыскания неопределенных коэффициентов может быть упрощена путем подстановки в левую и правую части равенства значений корней, например,

7. Решают СЛАУ и находят числовые значения неизвестных коэф-фициентов

Для рассматриваемого примера .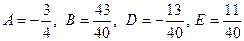

8. Числовые значения неопределенных коэффициентов подставляют в разложение правильной рациональной дроби на простые дроби (п.4 данной схемы) .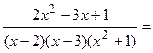

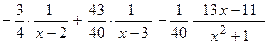9. Полученное разложение рациональной дроби на простые дроби ин-тегрируется .

Пример 6. Вычислить .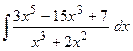

Подинтегральная функция представляет собой неправильную рациональную дробь, поэтому выделим “целую” часть и правильную рациональную дробь:

.

Разложив знаменатель правильной рациональной дроби на простые множители, представим эту дробь в виде суммы простых дробей:

.

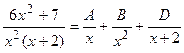Приводя сумму простых дробей к общему знаменателю и приравнивая числитель получившейся дроби к числителю исходной дроби, получим после раскрытия скобок и приведения подобных членов:

.

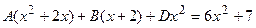Сравнивая коэффициенты при одинаковых степенях , получаем СЛАУ:

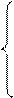
Таким образом, подинтегральную функцию можно представить в виде:

.

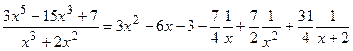Проинтегрируем полученное выражение

.

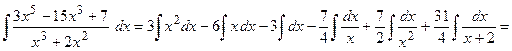
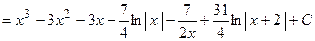Интегрирование последней дроби рассмотрено ниже.

3. Интегрирование простых дробей.

При интегрировании рациональных дробей возникают интегралы вида и 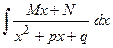с квадратичным полиномом, имеющим отрицатель-ный дискриминант 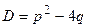. Интегралы первого вида путем замены сводятся к табличным интегралам 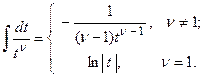. Интегралы второго вида 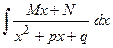вычисляются с помощью замены 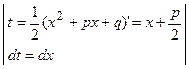, которая приводит к интегралу 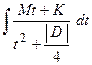, где 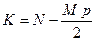. Использование метода тождественных преобразований подинтегральной функции позволяет записать этот интеграл в виде:

.

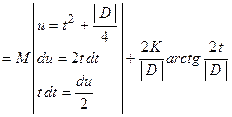
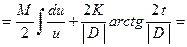
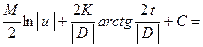
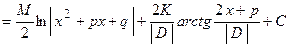Пример 7. Вычислить .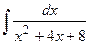

Воспользуемся указанной выше заменой

.

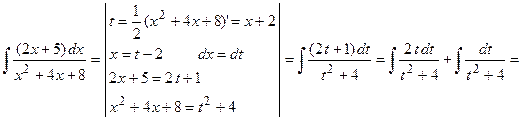
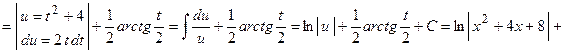
Лекция № 5 “Интегрирование тригонометрических функций”

1. Универсальная тригонометрическая подстановка.

При вычислении неопределенных интегралов от рациональной функции, зависящей только от тригонометрических функций применяется универсальная тригонометрическая подстановка, применение которой обосновано следующими формулами, связывающими функции синуса и косинуса с тангенсом половинного аргумента

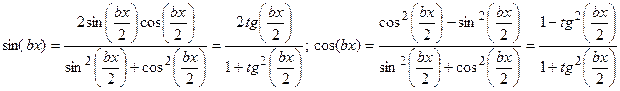
При вычислении 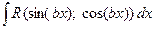проводят универсальную тригонометрическую подстановку . Из этих формул видно, что вне зависимости от величины параметра 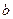формулы для синуса и косинуса носят универсальный характер.

Пример 1. Вычислить .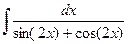

Воспользуемся универсальной тригонометрической подстановкой

.

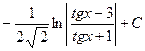З1. Отметим, что универсальную тригонометрическую подстановку следует применять не во всех случаях. Для некоторых типов интегралов от тригономнтрических функций, которые будут рассмотрены ниже, существуют более простые способы вычисления.

2. Интегралы вида (и 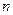– целые числа).

а) Если хотя бы одно из чисел или 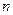является нечетным целым числом, то от нечетной степени отделяют один множитель, а оставшуюся четную часть выражают через другую тригонометрическую функцию с помощью основного тригонометрического тождества 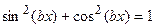, при этом надо помнить, что , а .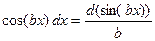

Пример 2. Вычислить .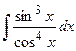

Согласно изложенному способу вычисления, получим

.

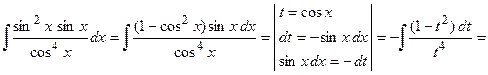
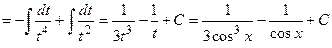Пример 3. Вычислить .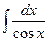

.

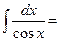
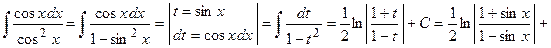
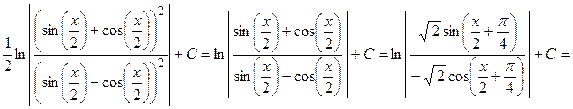
Пример 3. Вычислить (самостоятельно).

б) Если и 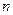являются четными неотрицательными целыми числами, то используют тригонометрические формулы понижения степени

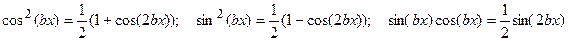
формулы подобия, например,

, …

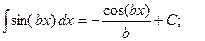
Пример 4. Вычислить .

.

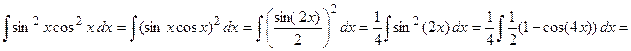
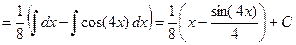3. Интегралы вида , ,.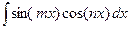

При вычислении таких интегралов используют формулы:

; ;

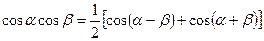
и формулы подобия: , ,...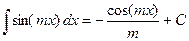

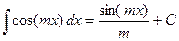Пример 5. Вычислить .

Так как и 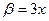(обратите внимание на тот факт, что величина 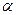всегда определяется по синусу при наличии косинуса), то

.

Пример 6. Вычислить .

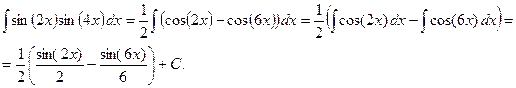
4. Интегралы вида и

(и 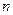– целые положительные числа).

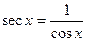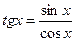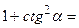
Напомним, что , , , . При интегрировании используются формулы ; , при этом надо помнить, что 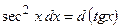и .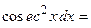

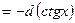Пример 7. Вычислить .

Преобразуем подинтегральную функцию к виду

.

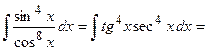
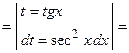
Частными случаями рассмотренных интегралов являются интегралы и (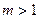). Такие интегралы вычисляются путем отделения квадрата подинтегральной функции и использованием вышеприведенных формул.

Пример 8. Вычислить .

.

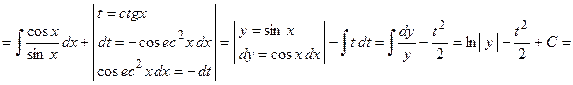
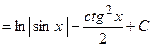5. Интегралы вида и

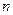(– целое положительное число).

Такие интегралы вычисляются по частям с использованием рекуррентных формул. Вычислим, например,

.

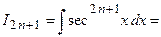
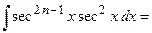
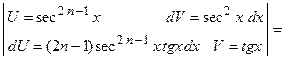
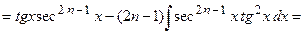
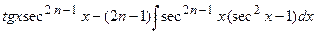
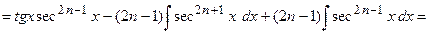
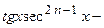
Решая это равенство относительно величины 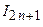, получаем

.

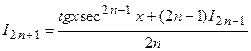О1. Соотношения полученного типа называются рекуррентными.

Рекуррентные соотношения позволяют по известному значению более низкого порядка вычислять значения искомой величины более высокого порядка. Аналогично полученному рекуррентному соотношению получают формулу для вычисления .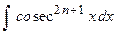

Пример 9. Вычислить .

Согласно рекуррентному соотношению получаем

.

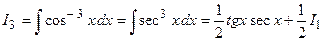Интеграл вычислен в п. 2а), поэтому окончательный ответ имеет вид

.

Дата добавления: 2014-01-11