
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В абсолютно сходящемся ряде можно произвольно переставлять его члены, при этом сумма ряда не изменится
|
|
|
|
З1. Отметим, что в зависимости от того, как группируются члены знакочередующегося ряда можно получить любое число, например, пусть дан ряд. Если сгруппировать его члены следующим образом, то получим, что его сумма равна единице, а если сгруппировать так, то получим, что его сумма равна нулю.
Пример 1. Исследовать на сходимость ряд 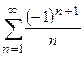 .
.
В развернутом виде данный ряд имеет вид 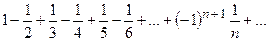 . Последовательность, составленная из абсолютных величин членов этого ряда, удовлетворяет обоим условиям признака Лейбница: а)
. Последовательность, составленная из абсолютных величин членов этого ряда, удовлетворяет обоим условиям признака Лейбница: а) 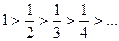 – монотонно убывает; б)
– монотонно убывает; б) 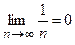 . Отсюда следует, что данный ряд сходится.
. Отсюда следует, что данный ряд сходится.
2. Абсолютная и условная сходимость знакопеременных ряда.
О2. Ряд, члены которого имеют произвольные знаки, называется знако-переменным или произвольным.
З2. Знакочередующиеся ряды являются частным случаем переменных рядов.
Пусть дан ряд 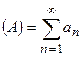 , члены которого могут быть отрицательными, нулевыми или положительными. Составим из модулей членов ряда
, члены которого могут быть отрицательными, нулевыми или положительными. Составим из модулей членов ряда 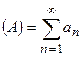 новый ряд
новый ряд 
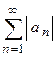 , т.е. этот ряд состоит только из положительных членов.
, т.е. этот ряд состоит только из положительных членов.
Т2. Если ряд 
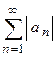 сходится, то сходится и ряд
сходится, то сходится и ряд 
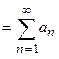 .
.
Док-во. Пусть ряд  сходится. Обозначим через
сходится. Обозначим через 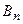 его
его  -ую частичную
-ую частичную
сумму. В силу того, что ряд  сходится, то
сходится, то 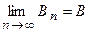 . Очевидно, что для любого числа
. Очевидно, что для любого числа  выполняется неравенство
выполняется неравенство  , так как члены ряда
, так как члены ряда  неотрицательны. Составим из ряда
неотрицательны. Составим из ряда  два ряда
два ряда 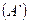 и
и 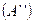 , составленные из положительных и отрицательных членов, соответственно. Обозначим частичные суммы этих рядов через
, составленные из положительных и отрицательных членов, соответственно. Обозначим частичные суммы этих рядов через  и
и 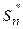 , соответственно. Тогда
, соответственно. Тогда  -ая частичная сумма ряда
-ая частичная сумма ряда  будет равна
будет равна 
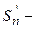
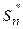 . Ясно, что последовательности частичных сумм
. Ясно, что последовательности частичных сумм  и
и 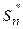 не убывают, так как члены рядов
не убывают, так как члены рядов 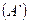 и
и 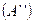 удовлетворяют неравенствам
удовлетворяют неравенствам  и
и 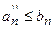 . Следовательно, по признаку сравнения из сходимости ряда
. Следовательно, по признаку сравнения из сходимости ряда  следует сходимость рядов
следует сходимость рядов 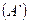 и
и 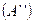 , т.е.
, т.е. 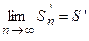 и
и 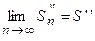 . Тогда
. Тогда 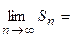
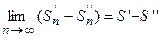 . Из полученного равенства следует, что ряд
. Из полученного равенства следует, что ряд  сходится.
сходится.
Пример 2. Исследовать на сходимость ряд 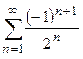 .
.
Составим ряд из абсолютных величин членов данного ряда, получим ряд 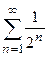 . Данная сумма представляет собой сумму бесконечной геометрической прогрессии с первым членом
. Данная сумма представляет собой сумму бесконечной геометрической прогрессии с первым членом 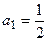 и знаменателем
и знаменателем 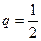 , которая равна
, которая равна 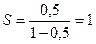 , т.е. полученный ряд сходится. По признаку сравнения сходится и исходный ряд.
, т.е. полученный ряд сходится. По признаку сравнения сходится и исходный ряд.
О3. Если ряд, составленный из модулей членов переменного ряда, сходится, то исходный переменный ряд называется абсолютно сходящимся.
О4. Если ряд, составленный из модулей членов переменного ряда, расходится, а исходный переменный ряд сходится, то переменный ряд называется условно сходящимся.
Пример 3. Исследовать на сходимость ряд 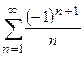 .
.
При 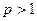 ряд, составленный из модулей членов знакочередующегося ряда, сходится (см. Лекцию № 19), следовательно, исходный ряд является абсолютно сходящимся. При
ряд, составленный из модулей членов знакочередующегося ряда, сходится (см. Лекцию № 19), следовательно, исходный ряд является абсолютно сходящимся. При  ряд, составленный из модулей членов знакочередующегося ряда, расходится, но по признаку Лейбница исходный переменный ряд будет сходиться, следовательно, исходный переменный ряд является условно сходящимся.
ряд, составленный из модулей членов знакочередующегося ряда, расходится, но по признаку Лейбница исходный переменный ряд будет сходиться, следовательно, исходный переменный ряд является условно сходящимся.
3. Свойства абсолютно сходящихся рядов.
|
|
|
Дата добавления: 2014-01-11; Просмотров: 710; Нарушение авторских прав?; Мы поможем в написании вашей работы!