Использование фильтра Калмана для ассимиляции гидрометеорологических данных

Задача ассимиляции как проблема фильтрации

В рассмотренных до сих пор методах ковариационные матрицы фоновых оценок (моделирования или прогноза) оценивались в начале однократно и затем использовались для всего последующего процесса ассимиляции. Однако практика показывает, что ошибка прогноза (моделирования) может меняться от дня ко дню. Таким образом, на повестку дня встает вопрос об учете временной эволюции ковариационной матрицы ошибок фоновых оценок (прогноза). Эволюция во времени фоновых ошибок может быть важной по трём причинам.

· Во-первых, мы можем отличить области, где в предыдущем анализе фоновые ошибки были уменьшены при помощи наблюдений.

· Во вторых, мы можем отличить области, где фоновые ошибки росли из-за модельных ошибок.

· В третьих, модельные физика и динамика могут и усилить и уменьшить фоновые ошибки.

Фильтр Калмана является таким методом, который позволяет на основе анализа, сходного с оптимальной интерполяцией, учесть изменчивость ковариационной матрицы прогноза состояния среды.

Проблема ассимиляции гидрометеорологических данных может рассматриваться как решение задачи фильтрации, где ошибки измерений и моделирования выступают в виде шума на фоне истинных значений, который необходимо отфильтровать, чтобы выделить сигнал. Одним из наиболее эффективных методов решения подобной задачи является фильтр Калмана.

Фильтр Калмана представляет собой рекурсивный фильтр, который позволяет оценить состояние динамической системы на основе неполных и шумящих измерений. Для оценивания состояния среды только на основе шумных (т.е. имеющих ошибки) измерений необходимо иметь модель эволюции среды. Рекурсивность фильтра Калмана означает, что для оценки состояния среды достаточно иметь предыдущую оценку и текущие измерения, отягощенные шумом. Другую информацию о предыдущих шагах хранить не надо.

Атмосфера является системой, состояние которой характеризуется определенным набором характеристик, которые являются элементами вектора состояния системы , отнесенного к заданному моменту времени. Кроме того, имеется ряд переменных, некоторым образом связанных с вектором состояния системы, которые можно измерить с определенной точностью и которые относятся к определенному моменту времени. Эти величины составляют вектор измерений . Задача формулируется как построение оптимальной оценки вектора состояния системы, основываясь на векторе измерений с погрешностями. При этом вектор измерений рассматривается как входной сигнал, отягощенный погрешностями (шумом), а вектор состояния - как неизвестный многомерный сигнал, подлежащий оценке. Задача решается как отфильтровывание шума (погрешностей).

Условием оптимальности построенной оценки состояния является минимум ее среднеквадратической ошибки. Рисунок иллюстрирует работу алгоритма фильтра Калмэна. Начальными условиями на каждом новом цикле алгоритма служат оценка состояния системы и величина, характеризующая ее погрешность. В случае скалярной переменной такой характеристикой является дисперсия, которая тем больше, чем сильнее разброс индивидуальных значений относительно истинного значения. Распространенная оценка дисперсии — среднеквадратическое отклонение, то есть квадрат стандартного отклонения, — выражает степень разброса величины относительно среднего. Обобщением дисперсии для вектора, то есть совокупности скалярных величин, служит ковариационная матрица. Ее диагональные элементы являются дисперсиями соответствующих составляющих вектора, а недиагональные — ковариациями, характеризующими взаимосвязь между парой составляющих. Совокупность измерений, отнесенных к каждому из моментов времени, обобщает вектор измерений. Алгоритм последовательно обрабатывает вновь поступающие векторы измерений, учитывая при этом значения, вычисленные на предшествующем цикле. Эта особенность отличает алгоритм фильтра Калмана от нерекуррентных алгоритмов, которым для работы требуется хранить весь массив обрабатываемых данных. На следующем шаге с помощью обрабатываемых на данном цикле измерений уточняются начальные условия.

Для этого алгоритм вычисляет вес поправок к ним на основе ковариационных матриц оценки состояния и измерений. Чем меньшей погрешностью характеризуются измерения по сравнению с оценкой состояния системы, тем больший вес они получат. Относительные веса неизвестных, определяющих вектор состояния системы, зависят от степени их влияния на вектор измерений: больший вес получат те переменные, вклад которых в измерения больше.

Фильтр Калмана является примером последовательного метода ассимиляции распределенных во времени данных измерений, что означает корректировку начальных данных для моделирования на каждом шаге модели в отличии от 4-мерного вариационного анализа который рассматривает все данные измерений внутри определенного окна ассимиляции.

Формулировка алгоритма фильтра Калмана

Рассмотрим сначала линейную задачу, т.е. вариации модельных предсказаний в окрестности предсказания являются линейной функцией начального состояния, т.е. для всякого , достаточно близкого к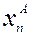

Модель использует данные анализа на сетке в момент времени для того, чтобы вычислить прогностические значения на той же сетке в момент времени :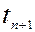

Предполагается, что модель может быть несовершенной и давать некоторую ошибку:

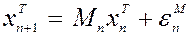
Из практики можно предположить, что ошибки не имеют сдвига и не коррелируют во времени:

где - символ Кронекера, равный 1 при и 0 при всех прочих случаях., 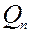- матрица ошибок модели в момент времени . Определим ошибку анализа в момент времени :

и вычислим ошибку прогноза с учетом линейности оператора моделирования

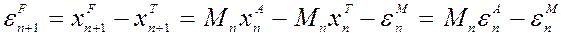
Возводя вквадрат, т.е., умножая левую часть на , а правую на , и полагая, что ошибки моделирования не коррелируют с ошибками анализа, т.е. , получаем

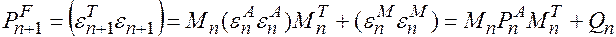
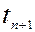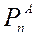где - ковариационная матрица ошибок прогноза в момент времени , а - ковариационная матрица ошибок анализа в момент времени .

В результате получены два прогностических уравнения для момента времени 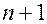на основании значений в момент времени 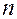: одно позволяет прогнозировать значение вектора состояния 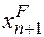, а второе ковариационную матрицу ошибок прогноза . Таким образом, использование методики фильтра Калмана позволяет рассчитывать как прогностические значения вектора состояния, так и ковариационную матрицу ошибок прогноза. Ковариационные матрицы ошибок прогноза и анализа являются идентичными матрицам ошибок оценки фонового состояния и анализа .

Прогностическая часть алгоритма должна быть дополнена уравнениями для вычисления результатов анализа вектора состояния, матрицы преобразования весов, а также ковариационной матрицы ошибок анализа. Эти уравнения аналогичны выведенным при рассмотрении обобщенного метода оптимальной интерполяции:

Эти три уравнения представляют собой аналитическую часть метода фильтра Калмана, а уравнения для прогноза вектора состояния и ковариационной матрицы ошибок – прогностическую часть фильтра Калмана.

Если у нас есть результаты измерений , ошибки измерений 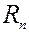, и ошибки моделирования 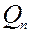, то начиная с начального момента времени 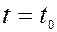, если определены 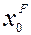и , то можно вычислить значения анализа в этот момент времени 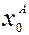и ошибки анализа 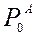. Затем, используя прогностические уравнения, можно вычислить для следующего момента времени прогностические значения вектора состояния и ковариационную матрицу ошибок прогноза . После этого последовательность повторяется, т.е. вычисляются и 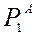и т.д для последующих моментов времени.

Фильтр Калмана аналогичен оптимальной интерполяции в части анализа и четырехмерному вариационному анализу в прогностической части, если не учитывается ошибка моделирования.

Расширенный фильтр Калмана

Если оператор модели нелинеен, то используется расширенный фильтр Калмана, в котором оператор 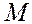линеаризуется в окрестности анализируемого вектора состояния 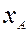, а оператор наблюдений линеаризуется около . Таким образом, подразумевается, что

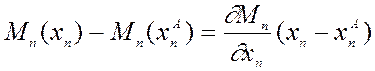
Это означает, что при вычислении ошибки прогноза мы должны учитывать Якобиан оператора моделирования:

Соответственно, прогностическое уравнение для ковариационной матрицы прогноза будет выглядеть как

Вычислительная стоимость фильтра Калмана и его расширенного варианта получается достаточно большой, т.к. помимо собственно анализа, который, как было определено при исследовании оптимальной интерполяции, занимает много процессорного времени и памяти, нужно еще оценивать матрицы ковариаций анализа, делать прогноз вектора состояния, вычислять Якобиан для нелинейной модели и прогноз изменения матрицы ковариаций анализа. В результате вычислительная стоимость фильтра Калмана намного больше 4-мерного вариационного для той же задачи, даже для малых моделей.

Схема организации вычислений в фильтре Калмана

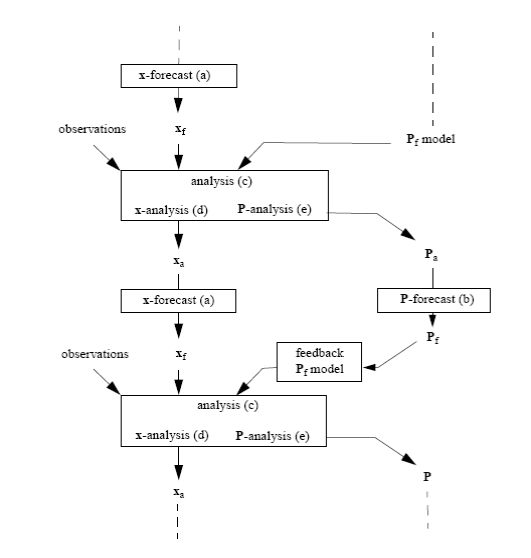
Ансамблевый фильтр Калмана

Из-за сложности процедуры использования фильтра Калмана в многомерных, нелинейных системах используются его упрощения.

а) Комбинация 4-мерного вариационного метода и фильтра Калмана. Если в качестве окна ассимиляции брать модельный шаг, то 4-Д Вар метод позволяет эффективно вычислять ковариационную матрицу ошибок анализа, избегая большого числа вычислений при оценке ее обычным способом. Затем можно использовать фильтр Калмана для прогноза ковариационной матрицы ошибок прогноза в следующий момент времени.

б) Ансамблевый фильтр Калмана.

Используется ансамбль анализов вектора состояния среды

,

по которым на каждом временном шаге, с помощью оператора моделирования рассчитывается ансамбль первых приближений:

Используя полученный ансамбль первых приближений можно оценить среднее значение вектора состояния

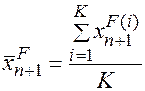
И ковариационную матрицу ошибок первого приближения

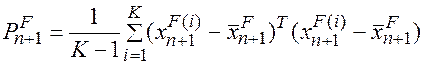
Для построения ансамбля анализов используется ковариационная матрица ошибок анализа

Для упрощения процедуры часто используется локализация, когда рассматриваются ковариации только между компонентами вектора состояния, расположенными на ограниченном расстоянии от узла анализа.

Кроме того, часто помимо ансамбля анализа используются также и возмущенные наблюдения, когда формируются 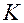наборов наблюдений, сгенерированных согласно матрице ошибок наблюдений .

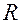Простой пример фильтра Калмана

Основные мысли предыдущего раздела поможет прояснить следующий простой пример. Рассмотрим задачу вывода реальной температуры воздуха номиналом 20 градусов из повторных измерений термометром и их обработки фильтром Калмэна. В первую очередь необходимо установить модели, связывающие состояния нашей системы с измерениями и между собой, а также их статистические характеристики, служащие для вычисления весов. В данном случае имеет место всего одна величина, характеризующая неизменное состояние системы, — неизвестная температура x. Таким образом, модель, описывающая состояние системы, выглядит как

Т.е. температура не меняется от времени к времени. Предположим, что распределение температуры характеризуется нормальным распределением с дисперсией 4 градуса в квадрате (среднеквадратическое отклонение 2 градуса). Это можно принять как ошибку прогноза неменяющейся температуры, т.е.

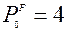
Измерения температуры термометром дают истинные значения температуры, отягощенные инструментальными ошибками

Если, в соответствии с документами прибора дисперсия составляет 1 градус в квадрате, то

тогда вес измерения составит

Результат анализа, т.е. исправленное значение будет

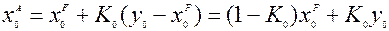
Таким образом, чем больше вес измерения 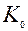, тем больше его вклад в результат нулевого анализа.

Ошибка анлиза будет характеризоваться его дисперсией

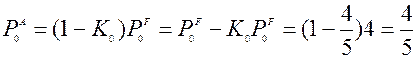
т.е. дисперсия прогноза за счет хорошего измерения существенно уменьшилась.

Это была аналитическая часть, далее идет прогностическая часть

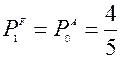
т.к. модель в данном случае являетя безошибочной.

Теперь опять часть анализа

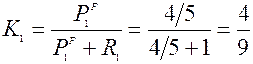
таким образом ошибка анализа еще больше уменьшилась.

Аналогичная последовательность операций продолжается и далее.

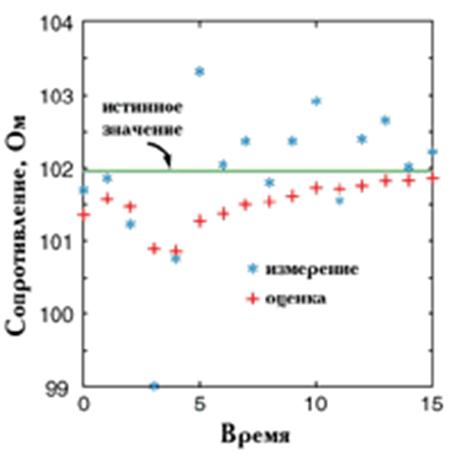
Рисунок показывает, как результат анализа сходится к истинному значению температуры в данной точке.

Дата добавления: 2014-01-11