Абсолютная и относительная погрешности

Источники и классификация погрешностей

При замене задачи (1) на задачу (2) получаемое решение отличается от истинного решения задачи (1), т.е. несет в себе некоторую погрешность.

Погрешность решения задачи обуславливается следующими причинами:

1) математичское описание задачи является неточным, в частности, неточно заданы исходные данные описания;

2) применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций, поэтому вместо точного решения задачи приходится прибегать к приближенному;

3) при вводе данных в машину, при выполнении арифметических операций, при выводе данных производятся округления.

Погрешности, соответствующие этим причинам, называют:

1) неустранимой погрешностью;

2) погрешностью метода;

3) вычислительной погрешностью.

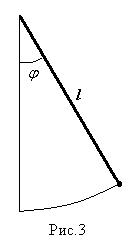Пример. Пусть имеется математический маятник (рис.3), который начинает свое движение в момент времени 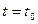. Требуется определить угол отклонения от вертикали в момент .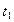

Дифференциальное уравнение, описывающее колебание маятника, берется в виде:

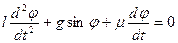, (3)

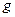где - длина маятника, - ускорение свободного падения, 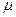- коэффициент трения.

Как только принимается такое описание задачи, решение уже приобретает неустранимую погрешность, в частности, потому, что реальное трение зависит от скорости не совсем линейно; другой источник неустранимой погрешности состоит в погрешностях определения , , 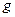, ,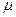, . Название погрешности – «неустранимая» соответствует ее существу: она неконтролируема в процессе численного решения задачи и может уменьшится только за счет более точного описания физической задачи и более точного определения входных параметров. Дифференциальное уравнение (3) не решается в явном виде, для его решения требуется применить какой-нибудь численный метод. Вследствие этой причины возникает погрешность метода. Вычислительная погрешность возникает из-за конечности количества разрядов чисел, участвующих в вычислениях.

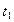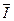Введем формальные определения. Пусть - точное значение отыскиваемого параметра (в данном случае – реальный угол отклонения маятника в момент времени ), - значение этого параметра, соответствующее принятому математическому описанию (математической модели) (в данном случае – значение точного решения уравнения (3)), - решение полученной математической задачи (в данном случае – уравнения (3)), получаемое при реализации численного метода в предположении отсутствия округлений, - приближение к решению задачи, получаемое при реальных вычислениях. Тогда

- неустранимая погрешность,

- погрешность метода,

- вычислительная погрешность,

- полная погрешность.

Полная погрешность удовлетворяет равенству

.

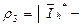
Возможно полагать , , 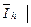. В таких обозначениях .

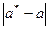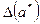Пусть - точное значение некоторой скалярной величины, а - известное приближение к нему. Тогда абсолютной погрешностью приближенного значения называется , а относительной - . Однако чаще всего точное значение неизвестно, поэтому далее под абсолютной (относительной) погрешностью будем понимать некоторую величину (), про которую известно, что

.

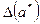
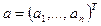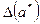Если - точное значение не скалярной, а векторной величины, т.е. , а - известное приближение к нему: , то, по аналогии со скалярной величиной, под абсолютной (относительной) погрешностью будем понимать некоторую величину (), про которую известно, что

,

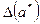
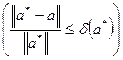где 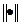- норма вектора-аргумента.

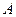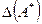Если - матрица, а - матрица приближения, то под абсолютной (относительной) погрешностью будем понимать некоторую величину (), про которую известно, что

,

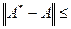
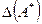
где 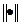- матричная норма.

Относительную погрешность часто выражают в процентах.

Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева.

Пример. У чисел , значащие цифры подчеркнуты.

Значащую цифру называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Пример. , ; 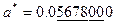, 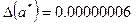. Подчеркнутые цифры – верные.

Если все значащие цифры верные, то говорят, что число записано со всеми верными цифрами.

Часто информация о некоторой величине задается пределами ее измерения:

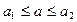(например, ).

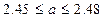Принято записывать эти пределы с одинаковым числом знаков после запятой.

Информация о том, что является приближенным значение числа с абсолютной погрешностью 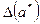, иногда записывают в виде

,

числа и 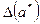принято записывать с одинаковым числом знаков после запятой. Например,

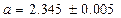
означает, что

.

Соответственно информацию о том, что является приближенным значение числа с относительной погрешностью , записывают в виде:

.

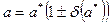Например, запись

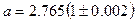
означает, что

.

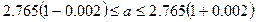Следует различать формально математическую и обиходную терминологии в рассуждении о величине погрешности. Если в постановке задачи говорится, что требуется найти решение с погрешностью , то чаще всего предполагается лишь, что погрешность имеет такой порядок. Если, например, решение будет найдено с погрешностью , то такой результат, скорее всего, также удовлетворит заказчика.

Дата добавления: 2014-01-11