Декартовы координаты

МЕТОДЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В 3-Х МЕРНОМ ЭВКЛИДОВОМ ПРОСТРАНСТВЕ

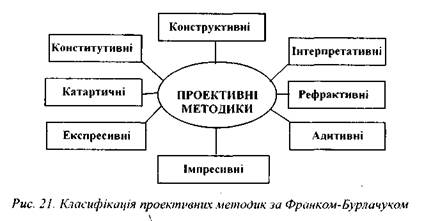
Класифікація проективних методик

Найвідомішою класифікацією проективних методик є класифікація, котра була запропонована Л.Франком та доповнена Л.Ф.Бурлачуком [39] (див. нижче рис. 21).

Висновки до лекції

Зав. кафедри ТМПП Проф. Варій М.Й.

Викладач кафедри ТМПП Терлецька Ю.М.

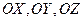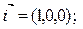
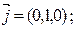
Будем считать, что в пространстве введены прямоугольные декартовы координаты. Пусть О (0;0;0) - начало координат - взаимно перпендикулярные оси; 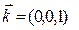- единичные орты этих осей.

Найдем их скалярные произведения:

, , ,

, , ,

, , .

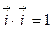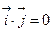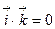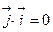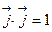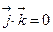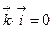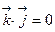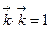Таким образом, векторы 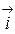, , 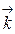образуют ортонормированный базис, поскольку и векторы 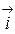, , 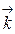ортогональны. Этот базис мы будем называть стандартным базисом пространства R ³.

Каждой точке М (x,y,z) соответствует радиус-вектор 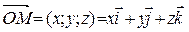,каждой паре точек 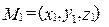, 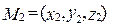соответствует вектор 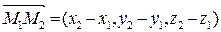. Если М ₁(х ₁, у ₁, z ₁) и М₂ (х ₂, у ₂, z ₂) – концы отрезка М ₁ М ₂, а точка М (х, у, z) делит этот отрезок в отношении 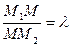, то координаты этой точки:

; ; .

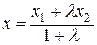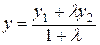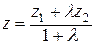Если М (х, у, z) – середина отрезка М ₁ М ₂, то 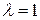и

, , .

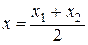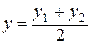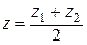Любой вектор обозначается двумя буквами 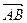с чертой или стрелкой над ними, причем первая буква указывает начало вектора, а вторая – его конец. Вектор может быть обозначен также одной буквой латинского алфавита , 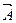. Длину или модуль вектора обозначают в виде 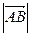, ||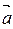. Вектор может быть приложен к любой точке А пространства.

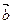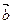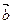Суммой двух векторов и называется третий вектор + , который идет из начала первого вектора в конец второго , если второй вектор выходит из конца первого (рис. 4.1)

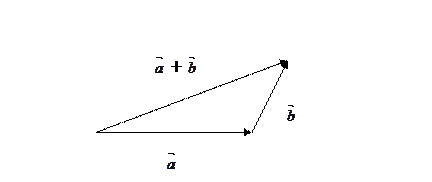
Рис. 4.1. Сложение векторов

Разностью двух векторов и 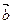называется третий вектор - 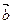, который представляет собой сумму вектора и вектора, противоположного вектору 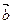, т.е. - 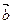= + (- 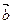) (рис. 4.2)

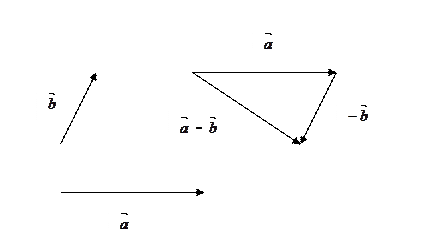
Рис. 4.2. Разность векторов

Произведением вектора на число λ называется вектор, обозначаемый λ, такой, что:

1) |λ| = |λ| ||;

2) векторы и λимеют одно направление, если λ > 0, и противоположное, если λ < 0.

Если вектор составляет угол φ с осью Ох, то проекцией вектора на эту ось называется произведение модуля вектора на косинус угла φ:

пр_х = || cos φ.

Проекция суммы векторов и 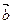на ось Ох равна сумме проекций этих векторов на эту ось:

пр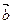_х (+ ) = пр_х + пр_х.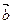

В трехмерном пространстве Oxyz вектор может быть представлен разложением по координатному базису в виде:

,

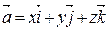где 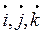- единичные базисные векторы, направление каждого из которых совпадает с положительным направлением соответствующей оси;

x, y, z – проекции вектора на оси координат.

Длина (модуль) вектора определяется через проекции по формуле:

.

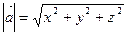Косинусы углов α, β, γ, образованных вектором с осями координат, находятся в виде соотношений

, , .

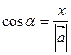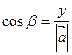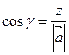Они называются направляющими косинусами.

Равенство = (x, y, z) используется для выражения вектора через его проекции на заданные координатные оси.

Векторы, лежащие на одной прямой или параллельных прямых, называются коллинеарными. Условие коллинеарности двух векторов = (x ₁, y ₁, z ₁) и 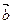= (x ₂, y ₂, z ₂) записываются в виде:

= λ,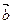

где λ – числовой множитель.

Через координаты это условие записывается в виде:

.

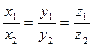Для каждой пары векторов 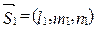; 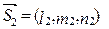определены:

а) скалярное произведение: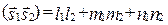

б) длина вектора 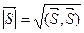, где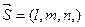

в) Углы между векторами вычисляются по формуле:

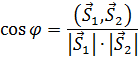
г) векторное произведение:

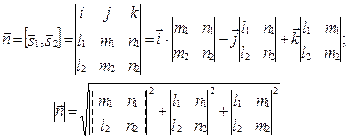
Свойства векторного произведения векторов 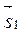и :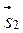

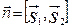
1) вектор 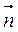перпендикулярен каждому из векторов 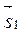и ;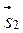

2) вектор 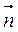направлен так, что если смотреть с его конца, то поворот первого вектора 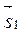ко второму вектору 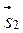на кратчайший угол 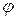проходит против часовой стрелки;

3) длина вектора 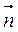равна площади параллелограмма, построенного на векторах 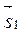и 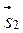, т.е. .

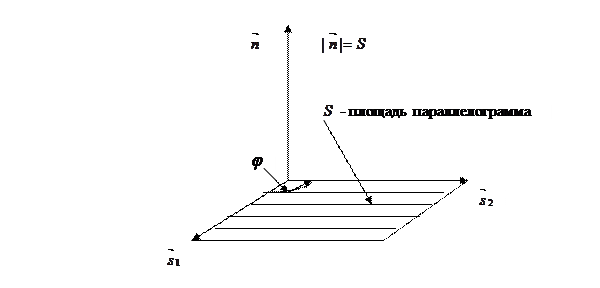
Рис. 4.3. Геометрический смысл векторного произведения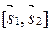

4) площадь треугольника, построенного на векторах 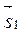и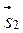, равна ;

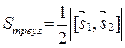5) ,

6) ,

7) ,

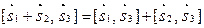8) если векторы 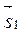и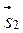коллинеарны, то 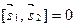. В частности, .

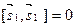д) смешанное произведение трех векторов 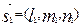,,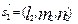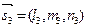есть число, обозначаемое

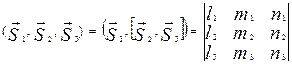
Геометрические свойства смешанного произведения:

a. Объем параллелепипеда (), построенного на векторах

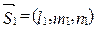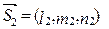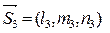,,определяется формулой: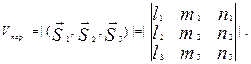

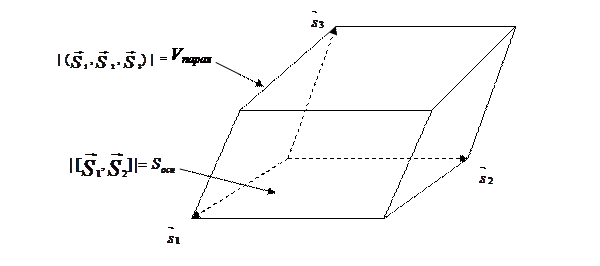Рис. 4.4. Геометрический смысл векторного и смешанного произведения

2) Объем пирамиды , построенной на векторах

,,:

.

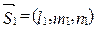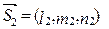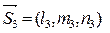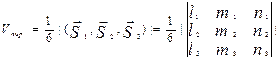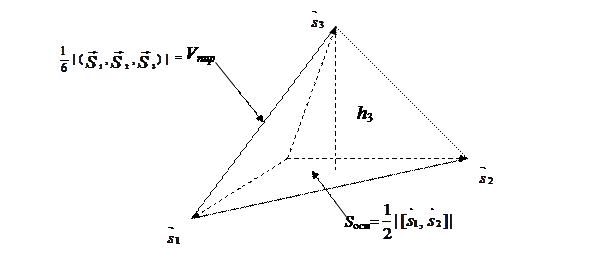
Рис. 4.5. Геометрический смысл векторного и смешанного произведения

3) Высота h ₃ пирамиды (параллелепипеда), построенной на векторах 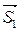,,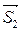, 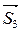(см. рис. 2.11) вычисляется по формуле:

.

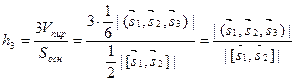4) Условие компланарности векторов

,,:

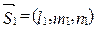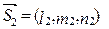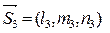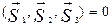или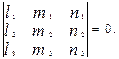

Векторы называются компланарными, если они лежат в одной плоскости.

Пример 4.1. Найти площадь параллелограмма, построенного на векторах = (–3, 2, 5) и 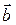= (1, 3, –2).

Решение. Сначала вычислим векторное произведение векторов и :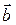

.

.

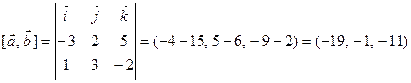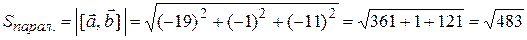Пример 4.2. Найти площадь треугольника АВС, если известны координаты его вершин: А (1, –1, 2), В (–3, 2, –1), С (4, 2, 1).

Решение. Можно считать, что треугольник АВС построен на векторах 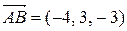и 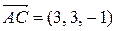. Вычислим векторное произведение этих векторов: .

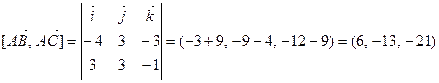Теперь найдем площадь треугольника АВС:

.

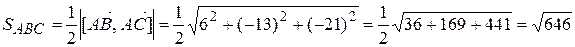Пример 4.3. Вычислить смешанное произведение векторов = (2, –1, 3), 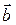= (1, 4, –2) и 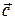= (–3, 2, 5).

Решение. Сначала вычислим векторное произведение векторов и :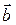

.

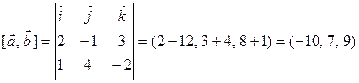Теперь вычислим смешанное произведение векторов , 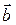и :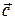

.

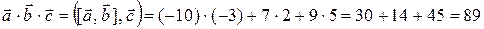Пример 4.4. А (3, –2, 5), В (1, 3, –2), С (0, 1, 1) и D (–4, 0, –3) – вершины пирамиды АВСD. Найти ее объем и высоту, опущенную из вершины D.

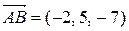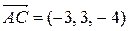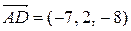Решение. Можно считать, что пирамида АВСD построена на векторах , и . Вычислим векторное произведение векторов 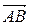и :

,

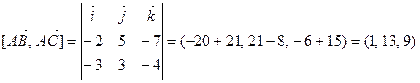а затем смешанное произведение векторов 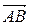, и :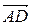

.

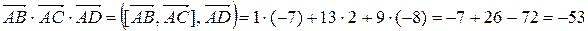Теперь найдем объем пирамиды АВСD:

.

.

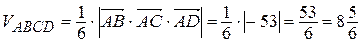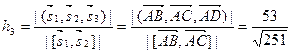Пример 4.5. Лежат ли точки А (3, –1, 2), В (–2, 2, 5), С (1, 4, 2) и D (0, 1, –2) в одной плоскости?

Решение. Если точки А, В, С и D лежат в одной плоскости, то векторы 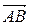, и 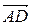– компланарны. В этом случае смешанное произведение векторов должно быть равным нулю. Вычислим смешанное произведение векторов 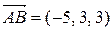, 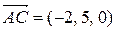и :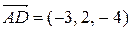

,

.

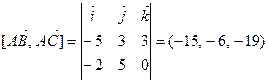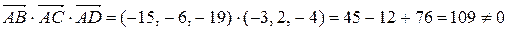Следовательно, векторы 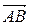, и 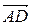не компланарны и, значит, точки А, В, С и D не лежат в одной плоскости.

Дата добавления: 2014-01-11