Завдання 1. На підприємстві мається одна площадка для розвантаження машин, що привозять сировину, і площадка для очікування на m машин

На підприємстві мається одна площадка для розвантаження машин, що привозять сировину, і площадка для очікування на m машин. Якщо всі місця на площадці очікування зайняті, то наступній машині, що прибула на підприємство, немає місця для очікування. Аналітично було з’ясовано, що на підприємство в середньому за хвилину прибуває потік машин інтенсивністю l, а потік обслугування з інтенсивністю m визначається тривалістю розвантаження.

Менеджера цікавить ймовірність відмови в обслуговуванні і середній час очікування в залежності від місць m.

Розв’язання

Дану задачу можна представити у вигляді одноканальної системи з обмеженою чергою. Число місць у черзі m. Якщо усі місця зайняті, то чергове замовлення, що надходить у систему, отримує відмову. Граф станів такої системи:

l l l l

m m m m

Рис.8.

Стани системи:

S₀ – канал вільний;

S₁ – канал зайнятий, іде обслугування, але черги немає;

S₂ – канал зайнятий, у черзі є одне замовлення;

S₃ - канал зайнятий, у черзі - два замовлення;

…

S_m+1 – канал зайнятий, у черзі знаходиться m замовлень.

Рівняння Колмогорова для такої системи:

l p₀ = m p₁;

(l + m) p₁ = l p₀ + m p₂;

… …

(l + m) p_m = l p_m-1 + m p_m+1;

p₀ + p₁ + p₂ + … + p_m + p_m+1 = 1.

Введемо позначення r = l / m, отримуємо імовірність вільного каналу:

р₀ = 1 / (1 + r + r ² + … + r ^m+1) = (1 - r) / (1 - r ^m+2);

p_k = r ^k × p₀,

де k = 1,2,3,…m+1.

Імовірність відмови - p_m+1.

Середня кількість замовлень у черзі:

де p_k - імовірність того, що у черзі знаходиться k-1 замовлення.

Середній час очікування у черзі: W_q=L_q / l.

Нехай інтенсивність прибуття машин l = 2,5, а інтенсивність обслуговування m = 1,5.

За результатами розрахунків у програмі MathCad отримуємо r = l / m = 1,667.

Якщо кількість місць у черзі m = 1, то імовірність відмови p_m+1 = 62,5%, а середній час очікування у черзі дорівнює 0,25 хвилин.

Якщо кількість місць у черзі m = 6 то імовірність відмови p_m+1 = 41,2%, а середній час очікування у черзі дорівнює 2,5 хвилин.

Видно, що якщо r > 1, то при великих m імовірність відмови стабілізується і стає рівною (r - 1) / r.

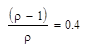
Щоб суттєво знизити імовірність відмови, необхідно (якщо неможна зменшити r) преходити до багатоканальної системи, тобто робити декілька площадок для розвантаження.

Дата добавления: 2014-01-11