Методы интегрирования

Лекция 12

1. Непосредственное интегрирование – вычисление интегралов с помощью таблицы простейших интегралов, правил интегрирования и свойств неопределенных интегралов.

Пример 1. + С.

Использована формула тригонометрии: .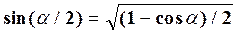

Пример2.

здесь выполнено очевидное преобразование подынтегрального выражения, и вместо переменной интегрирования х принято выражение (a–bx), относительно этой переменной получается табличный интеграл. Такой прием иногда называют «загонкой» под знак дифференциала некоторого выражения.

Действительно: .

2. Метод замены переменной. Метод подстановки.

Пусть y = f(x), x X. Введем новую переменную t, положив x = (t), t T, тогда y = f(x) = f((t)); dx = (t)dt и

.

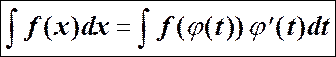После интегрирования последнего выражения нужно в результате перейти к старой переменной.

Этот метод применяется, когда подынтегральная функция является сложной функцией.

Пример. Найти интеграл :.

Решение.

1. Замена переменной: х=t/4, тогда dx=dt/4.

Подставив х и dx в исходный интеграл, получим:

= .

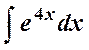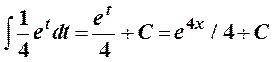2. Подстановка: 4х = t, тогда dx = dt/4. Получим тот же ответ.

3. Метод интегрирования «по частям».

Пусть в промежутке Х заданы две непрерывно дифференцируемые функции u(x) и v(x).

Запишем выражение для дифференциала их произведения:

.

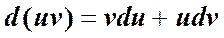Проинтегрируем левую и правую части полученного выражения:

,

отсюда следует формула интегрирования по частям:

.

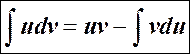Метод интегрирования по частям применяют для целого класса интегралов, например, когда подынтегральная функция содержит:

1) какую-либо функцию, которой нет в таблице простейших интегралов:

,

или ее произведение на многочлен P(x):

, .

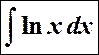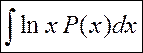В этом случае за u принимают, соответственно, 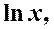, 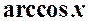и т. д., а за dv – выражение P (x) dx., так что одна из первообразных v легко может быть определена: ,

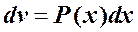(здесь при интегрировании произвольную постоянную следует опустить);

2) произведение многочлена на тригонометрическую функцию или на экспоненту: .

В этом случае за u следует принять P(x), а за dv – остальную часть подынтегрального выражения: exdx, sin xdx, и т.д.

Операцию интегрирования по частям можно применять многократно, что иногда позволяет решить задачу.

Пример 1. Найти интеграл .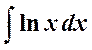

Решение.

Положим ln x = u, dx = dv (здесь P (x) = 1).

Тогда du = d (ln x) = , v = 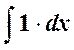= x – одна из первообразных.

Используя формулу интегрирования по частям ,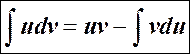

получаем:

= xln x – = x ln x – = x ln x – x + C = x (ln x – 1) + C.

Пример 2.

Найти интеграл .

Решение.

Пусть x = u (P(x) = x), 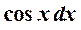= dvdu = , v =.

Используя формулу интегрирования по частям, получаем:

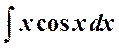= x sin x – = x sin x + cos x + C.

Пример 3. Найти интеграл .

Решение.

Положим x = u, e^xdx = dv.

Тогда du = dx, v = ex.

По формуле интегрирования по частям получаем:

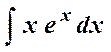= xe^x – = xe^x– e^x = e^x (x – 1) + С.

Пример 4. Найти интеграл .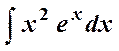

Решение.

Положим x ² = u, e^хdx = dv.

Тогда du = 2xdx, v = e^x.

По формуле интегрирования по частям получаем:

= x ²∙e^x – 2 .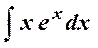

Применим еще раз интегрирование по частям (см. пример 3):

x ²e^x – 2 = x²e ^x – 2(xe ^x – e^x) + C =

= e^x(х² – 2x + 2) + C.

4. Метод неопределенных коэффициентов

Применяется для интегрирования рациональных функций

,

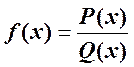где и – многочлены, и степень числителя меньше степени знаменателя (правильная дробь), неправильную дробь можно путем деления многочлена на многочлен свести к сумме некоторого многочлена и правильной дроби.

По теореме из алгебры, всякий многочлен степени n со старшим коэффициентом, равным единице, имеющий действительные различные корни x₁, x₂,..., x_n, можно представить так:

Q (x)=(x – x₁)(x – x₂)(x – x_n).

Тогда правильную дробь можно разложить на простейшие дроби и записать:

=,

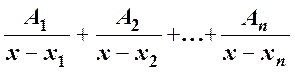где A₁, A₂,..., A_n – некоторые числа (неопределенные коэффициенты).

Приведя правую часть выражения к общему знаменателю и приравняв затем коэффициенты при одинаковых степенях х в числителе левой и правой части, получим систему уравнений для определения неизвестных коэффициентов A₁, A₂,..., A_n.

После этого интегрирование рациональной функции сводится к нахождению n интегралов вида:

.

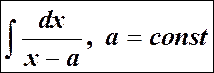Пример. Найти интеграл .

Решение. Подынтегральная функция есть правильная дробь, разложим ее на простейшие дроби.

Знаменатель имеет вещественные, различные корни: x₁ = 0, x₂ = 2, x₃ = –2. Следовательно, x3–4x = x (x–2)(x + 2),

.

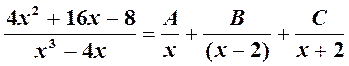Приведем правую часть последнего выражения к общему знаменателю и приравняем числители:

.

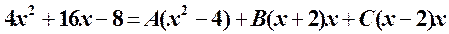
Приравниваем коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества:

отсюда определяем неопределенные коэффициенты разложения A, B, C:

A = 2, B = 5, C = – 3.

Следовательно,

= =

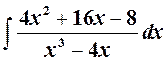= 2ln | x |+ 5ln | x–2 |–3 ln | x + 2 |+ C =

.

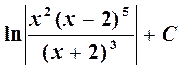Мы познакомились лишь с некоторыми наиболее часто используемыми приемами вычисления неопределенных интегралов, которые не охватывают всех случаев и не дают общих правил интегрирования. Кроме того, известны элементарные функции, для которых первообразная не является элементарной функцией (не выражается через простейшие функции с помощью конечного числа арифметических действий и суперпозиций).

Для таких функций интегрирование не может быть выполнено в конечном виде, т.е. в виде аналитической формулы, хотя ясно, что эти интегралы реально существуют. Интегралы, которые не выражаются через элементарные функции, называют “неберущимися”. На практике их вычисляют приближенными методами. Примеры “неберущихся” интегралов:

.

Нет общих признаков, на основании которых можно было бы определить, берется ли данный интеграл в конечном виде.

Задание:. Повторить основные формулы тригонометрии:

; ;

; ;

; ;

; ;

;

;

.

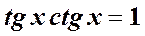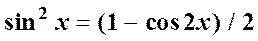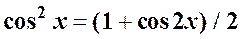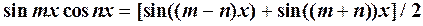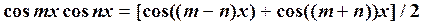Найти неопределенные интегралы (см. нижеприведенную таблицу):

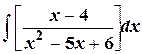
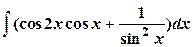
1.	2.	3.
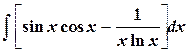
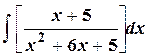
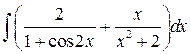
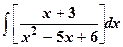
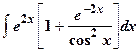
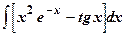
4.	5.	6.
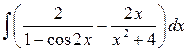
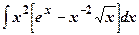
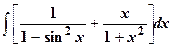
7.	8.	9.
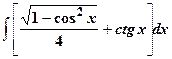
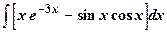
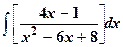
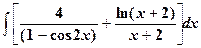
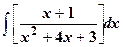
10.	11.	12.
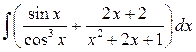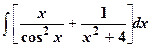
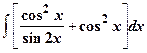
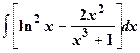
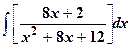
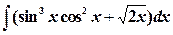
13.	14.	15.
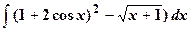
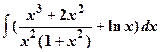
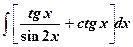
16.	17.	18.
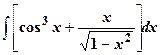
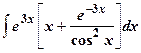
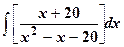
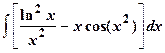
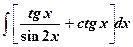
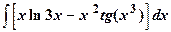
19.	20.	21.

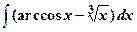
Дата добавления: 2014-01-11