Решение. 1) z. Данная формула имеет смысл, если х и у удовлетворяют неравенству: y–2x0

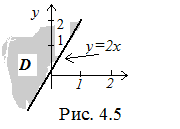
1) z . Данная формула имеет смысл, если х и у удовлетворяют неравенству: y–2x0, или y 2x, следовательно D ={ (x,y) | y2x }.

Областью определения является верхняя полуплоскость, включая прямую y = 2x (рис. 4.5).

Областью значений является промежуток: Е= [0,).

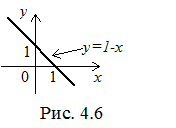
2) z = . Формула имеет смысл при x + y–10 или x + y1.

Следовательно D = { (x,y) | y + x1 }.

Областью определения являются все точки плоскости (0xy), не лежащие на прямой x + y = 1 (рис.4.6).

Областью значений является объединение промежутков: Е=(–,0 )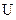(0,+).

3) z = y + arcsin(x + 2). Формула имеет смысл при – у + и –1 (х + 2) + 1. Следовательно

D = { (x,y) | y (–,+ ), | x + 2 |1}

Областью определения является бесконечная полоса на плоскости (хоу) с прямыми

х= –3 и х= –1 (рис. 4.7).

Областью значений является промежуток: Е =(–,+).

4) z = ln(x 2 + y 2 –1).

Формула имеет смысл при

х2 + у2–1>0, или х2 + у2>1.

Следовательно:

D ={ (x,y) | y2 + x2>1 }

Областью определенияявляется плоскость (хоу)

с исключенным замкнутым кругом единичного радиуса

х2 + у2 = 1 (рис. 4.8).

Областью значений является промежуток:

Е = ( –,+ ).

5) z 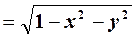.Формула имеет смысл при

1 – х2 – у20, или х2 + у2 1.

Функция определена на компакте:

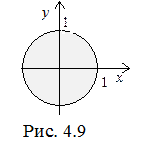
D = { (x,y) | y2 + x2 1 } (Рис.4.9).

Областью значений является отрезок: Е = [ 0,1 ].

Графики функций двух переменных представляют собой поверхности, определяемые уравнением z = f(x,y). Их эскизное построение часто является непростой задачей (примеры 1–5).

Существует еще один способ изображения функции двух переменных – с помощью линий уровня.

Линии уровня. Линией уровня (изолинией)поверхности z = f(x,y) называется проекция на плоскость 0xy сечения этой поверхности плоскостью, параллельной плоскости 0xy.

Иными словами, линией уровня функции z = f(x,y) называется геометрическое место точек поверхности, в которых функция принимает одно и то же значение С.

Совокупность линий уровня определяет характер изменения функции. В частности, если изменять С с постоянным шагом h, то там, где функция z изменяется быстрее, изолинии гуще, а где z изменяется медленнее, изолинии реже.

Выбирая h достаточно малым, можно по линиям уровня получить представление о характере поведения функции.

Этот способ применяется в топографии при составлении топографических карт для изображения рельефа местности, в теплофизике при исследовании тепловых процессов изображают изолинии температур – изотермы, в механике сплошных сред при изучении, например, напряженно-деформированного состояния нагруженной конструкции строят изолинии главных (наибольших и наименьших) напряжений и деформаций и т. д.

На рис. 4.10 показан график функции z 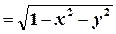(полусфера) и три её изолинии:

– сечение полусферы плоскостью z = 0 даст окружность радиуса 1;

– сечение полусферы плоскостью z = 0,5 даст окружность радиуса 0,866:

;;

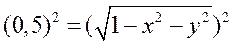– сечение плоскостью z = 1 даст вырожденную изолинию –точку.

Определение. (Функция трех переменных)

Переменная u называется функцией трех переменных (х,у,z), если каждой упорядоченной тройке чисел (х,у,z) D по определенному закону ставится в соответствие число u: u = f(x,y,z).

Областью определения функции трех переменных D является все трехмерное пространство или его часть.

Аналогично можно дать определение функции четырех переменных v = f (x,y,z,t). В этом случае каждый набор чисел (x,y,z,t) определяет “ точку ” в “ четырехмерном пространстве ” x,y,z,t. Такой точке и такому пространству нельзя дать геометрической интерпретации. Точка – это набор чисел (x,y,z,t ), а пространство – это совокупность всех таких наборов.

Областью определения (x,y,z,t) функции четырех переменных является четырехмерное пространство или его часть.

Можно рассмотреть множество D упорядоченных систем из n чисел (х₁, х₂,..., хn) и ввести понятие функции n переменныхна множестве D, здесь D – n -мерное пространство.

Определение. (Функция n переменных)

Переменная w называется функцией n переменных x₁, x₂,...,x_n, если каждой системе из n чисел (x ₁, x ₂,..., x _n) из множества D по определенному правилу или закону f ставится в соответствие некоторое значение (число) w:

w = f(x₁, x₂ ,..., x_n).

Областью определения функции n переменных D является n -мерное пространство или его часть.

Областью значений Е является промежуток:

Е = { w | w = f (x₁,x₂,...,x_n ) }.

Дата добавления: 2014-01-11