Результаты А. Лотце

Оптимизация структуры многозвенных систем.

Обычно при синтезе звеньевых КС используют уже существующие, несколько вариантов построения, выбирая из них оптимальный. Иногда используя опыт и интуицию проектировщиков. При этом рассматривают процесс синтеза начинают с неблокирующей структуры, в которой удаляют отдельные связи, добиваясь требуемого качества.

В качестве критерия оптимальности КС чаще всего используют число ТК.

Рассмотрим метод оптимизации звеньевых схем, предложенный А. Лотце по числу ТК на один Эрланг обслуженной нагрузки.

Метод рассчитан для КС, не имеющих существенной концентрации в промежуточных звеньях, за исключением первого и последнего.

На первом звене предполагается расширение, т.е. s₁>1, а на последнем концентрацию - s_s<1.

Метод оперирует двумя характеристиками:

а₁ – нагрузка, обслуживаемая одним входом первого звена;

Т – прозрачность схемы (ассоциируется с потерями).

Число ТК на один Эрланг обслуженной нагрузки – С:

,

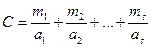где: m_i – число выходов одного коммутатора i-го звена;

а_i – нагрузка обслуживаемая одним входом i-го звена.

Под прозрачностью схемы понимается среднее число свободных путей в схеме между заданным входом и всеми М выходами схемы – Т.

,

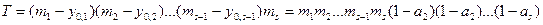где: у_0,i – нагрузка, обслуживаемая m_i выходами i-го звена;

а_i – нагрузка, обслуживаемая одним входом i-го звена.

Выражая из последнего выражения m, и подставляя его в формулу для С, имеем:

.

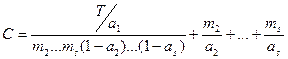При синтезе блокирующих КС величина нагрузки а₁ считается заданной. Смысл оптимизации заключается в подборе параметров m₂, …,m_s и величин а₂,…а_s, при которых минимизируется величина С при постоянной прозрачности схемы Т, гарантирующей требуемое качество обслуживания.

Таким образом, оптимизация заключается в решении 2(s-1) дифференциальных уравнений:

.

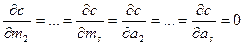В результате получаем основные формулы, используемые для оптимизации КС:

; ; ; .

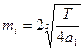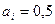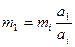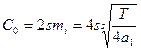Приведенные формулы справедливы при i=2,3,4, …,s и заданного числа s звеньев КС.

Оптимальное число звеньев s_опт:

,

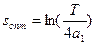а минимальное число точек коммутации на один Эрланг обслуженной нагрузки:

.

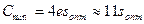В процессе оптимизации считаются заданными общее число входов – N, число выходов – М, нагрузка на один вход и прозрачность схемы – Т. Используя приведенные формулы для s_опт или любого другого числа звеньев определяют структурные параметры схемы, нагрузку на входы, исключая первый, и число точек коммутации на один Эрланг С₀ или С_min.

Дата добавления: 2014-01-11