Метод вероятностных графов

Расчет потерь в многозвенных коммутационных системах.

Автором метода является американский ученый Ли. Согласно этого метода КС представляется в виде графа, конфигурация которого определяется в основном структурой схемы и используемого режима искания.

Под графом будем понимать совокупность вершин и ребер, которые представляют собой множество путей в КС.

По виду графы подразделяются на параллельно-последовательные и мостиковые.

Приведем несколько примеров построения графов различных КС. На рис. 6.8 приведены вероятностные графы КС, изображенной на рис. 6.3, в режиме индивидуального – И, группового – Г и свободного – С искания.

Рис. 6.8 – Вероятностные графы 3-хзвенной КС.

Рис. 6.9 представляет собой вероятностные графы КС, представленной на рис. 6.5, работающей в тех же режимах искания.

Рис. 6.9 – Вероятностные графы 4-хзвеной КС.

На приведенных графах вершины представляют собой входы, коммутаторы и выходы КС, а ребра – промлинии между звеньями.

Потери в КС, имеющих параллельно-последовательные графы, определяются правилом сложения вероятностей.

Для схемы, имеющей граф, изображенный на рис. 6.8 а:

,

для схемы рис. 6.9 а:

.

Из приведенных рисунков видно, что в непараллельно-последовательных графах существенную роль играет простейший мостиковый граф, показанный на рис. 6.8 в. Потери в КС, имеющей такой граф, определяются следующим выражением:

.

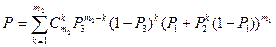В приведенных выше формулах неизвестны величины P_i (вероятности занятости ребер графа). Эти величины определяются с помощью следующих выражений:

; ; .

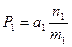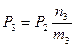где: а₁ – нагрузка, поступающая на один вход КС (обычно задается).

В тех случаях, когда вычисление потерь для мостиковых графов слишком громоздко, можно пользоваться методом оценочных графов.

В этом случае для рассматриваемого мостикового графа подбирается два параллельно-последовательных графа таким образом, чтобы вероятность потерь для одного из них была оценкой сверху для потерь в искомом графе, а потери для другого – оценкой снизу.

Тогда искомая вероятность потерь будет заключена между этими оценками.

В заключение отметим, что точность рассмотренного метода возрастает с увеличением числа звеньев. На практике этим методом можно рассчитывать потери в многозвенных КС, начиная с трехзвеньевых схем.

Дата добавления: 2014-01-11