Методы КЛИГС и ППЛ

Расчет потерь в многозвенных коммутационных схемах.

Немецкими специалистами во главе с проф. А. Лотце разработаны инженерные методы расчета многозвенных структур, которые по существу являются модификацией, рассмотренного выше, метода эффективной доступности. Наиболее часто используются две версии метода:

КЛИГС – расчет звеньевых схем группового искания;

ППЛ – расчет звеньевых схем индивидуального искания.

Метод КЛИГС оперирует следующими понятиями:

- средняя доступность (свободный веер),

- средняя недоступность (занятый веер),

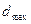- максимальная доступность (максимальный веер).

С помощью этих понятий определяется эффективная доступность 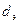, т.е. доступность однозвенной неполнодоступной КС.

Далее осуществляется расчет однозвенной НД схемы с помощью любого априорного метода (раздел 5.5). Авторы метода использовали для этого модифицированный метод Пальма – Якобеуса (метод МПЯ).

При этом используются следующие структурные параметры исходной звеньевой КС:

m_i – число выходов коммутатора i-го звена;

k_i – число коммутаторов на i-ом звене;

s – число звеньев;

q_r - число выходов одного коммутатора последнего звена в направлении r;

v_r – число линий в пучке направления r;

М – общее число выходов КС;

V_i,i+1 – число ПЛ между i и i+1 звеньями;

- коэффициент расширения на входе;

N – общее число входов КС;

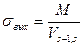- коэффициент концентрации на выходе.

Тогда

,

где: у_i – нагрузка, обслуживаемая одним коммутатором i-го звена.

На величину d_ср накладывается следующее ограничение:

,

которое означает, что средняя доступность коммутаторов любого звена от любого свободного входа не может превышать числа коммутаторов в соответствующем звене.

Физически величина d_ср представляет собой среднее число коммутаторов последнего звена, доступных для заданного входа в КС.

Максимальная доступность равна максимальному числу коммутаторов последнего звена, доступных заданному входу КС:

средняя недоступность:

характеризует среднее число недоступных коммутаторов последнего звена по отношению к заданному входу.

Эффективная доступность определяется как сумма двух слагаемых:

,

где:

, .

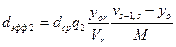где: y_or – нагрузка, обслуживаемая в направлении r.

у₀ – общая обслуживаемая нагрузка КС.

В соответствии с методом МПЯ потери определяются выражениями:

, , .

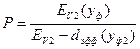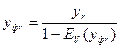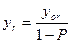Точность метода КЛИГС проверена методом статистического моделирования. Метод позволяет определить потери в КС, в которых число ПЛ между всеми звеньями одинаково, а d_вх³1 и d_вых£1, при этом рассматриваемые КС могут иметь любую структуру.

В методе ППЛ используется эквивалентность работы s-звенной КС в режиме И работе (s-1) звенной КС в режиме Г. Это положение иллюстрируется на рис. 6.10, где показана оконечная часть s-звенной КС.

Рис. 6.10 – Оконечная часть s-звенной КС.

Из рисунка видно, что работа s-звенной схемы при соединении с требуемым выходом (режим И) эквивалентна работе (s-1) звенной схеме при соединении с любым свободным выходом из числа - n_s в направлении j (режим Г). Поэтому все формулы, рассмотренные при описании метода КЛИГС справедливы для метода ППЛ.

Дата добавления: 2014-01-11