Моделирование случайных величин

Моделирование систем массового обслуживания связано с моделированием случайных ве­личин, имеющих различные распределения: равномерное, показательное, нормальное и др. Для получения таких случайных величин (СВ) используются СВ Х, равномерно рас­пределённая на отрезке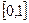, из которой с помощью различных преобразований получают СВ, подчиняющуюся требуемому распределению.

Случайная величина Х называется равномерно распределенной на отрезке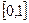, если её плотность f (c) на этом отрезке постоянная и равна единице:

Плотность распределения СВ иногда называют дифференциальной функцией рас­пределения СВ. Интегральная функция распределения (далее просто функция распределе­ния) этой СВ имеет следующий вид:

Плотность f(c) и функция распределения F(c) случайной величины Х, равно­мерно распределённой на отрезке 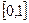, показаны на рис. 9.1

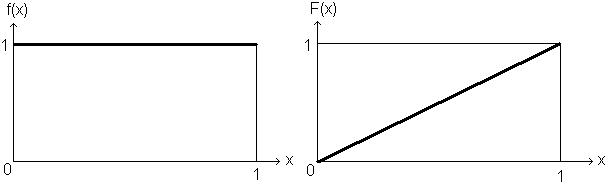
Рис.9.1- Плотность и функция распределения СВ,

равномерно распределенной на единичном отрезке.

СВ Х, равномерно распределённую на отрезке 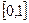, можно получить из дискретной СВ, равновероятно принимающей значения 0 и 1.

Рассмотрим двоичную дробь:

Х=0, а –1, a –2, …,

где: а –1, a –2, …, есть последовательность независимых СВ, каждая из которых с вероятностью 0,5 принимает значение 0 и с такой же вероятностью единицу, т.е. предос­тавляет дискретную СВ, равновероятно распределенную на отрезке .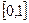

Для того чтобы промежутки между соседними значениями равномерно распреде­ленной СВ Х стремились к нулю, необходимо иметь бесконечную последовательность не­зависимых СВ (аi, i = -1, -2, …) равновероятно принимающих значения 0 и 1. На практике не­прерывно распределенная СВ моделируется приближенно. При этом может быть достиг­нута сколь угодно высокая точность за счет выбора числа К двоичных разрядов в ЭВМ, определяющих двоичную дробь

0, а –1, a –2, …, а -к

Таким образом, вместо непрерывной СВ, равномерно распределенной на отрезке 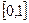, моделируется дискретная СВ, равновероятно принимающая значения

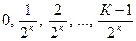
С промежутками между соседними значениями 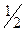К.

Случайные величины Х, равномерно распределённой на отрезке [0,1] обычно полу­чают программным путем на ЭВМ (псевдослучайные числа).

Псевдослучайные последовательности вырабатываются рекуррентным способом по алгоритмам, в которых каждое последующее число получается из предыду­щих в результате применения некоторых арифметических и логических операций. Эти последовательности называются псевдослучайными, т.к. они являются периодическими. Однако период может быть выбран столь большим, что практически этот недостаток можно не учитывать.

Возможность моделирования СВ Х, равномерно распределённой на отрезке 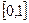, по­зволяет моделировать и непрерывную СВ x, распределенную по любому закону

F(x) = P (x<ζ)

Функция распределения СВ x монотонно возрастает от 0 до 1. можно показать, что значение СВ x, распределенную по любому закону в интервале [а, b) с плотностью f(x), определяется из уравнения.

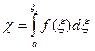(9.1)

Для каждой реализации величины Х решается уравнение(9.1) относительно x 1, т.е. определяется реализация величины x.

Эта процедура показана на рис 9.2.

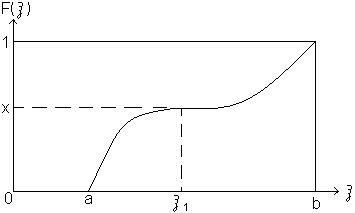
Рис 9.2. - К определению СВ x.

Для каждой конкретной реализации равномерно распределенной СВ Х пря­мая F(x) = c пересекает кривую функции распределения только в одной точке, абсцисса ко­торой x 1, и определяет значение x в этой реализации.

Рассмотрим принцип моделирования СВ x, равномерно распределенной в интер­вале [a, b), и СВ, распределенной по конкретному закону. Равномерно распределенная в интервале [а, b) СВ имеет в этом интервале постоянную плотность, равную

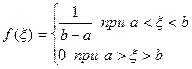
Согласно (9.1)

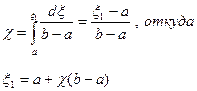(9.2)

Используя в процессе моделирования каждую реализацию СВ Х и преобразование (9.2), получаем последовательность СВ x, равномерно распределенных в интервале [a, b).

СВ x,распределенная в интервале [0, ¥) по показательному закону с параметром l имеет плотность распределения

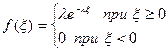
Согласно (9.1)

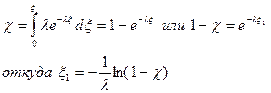
Величина (1 - c) точно так же, как и c, является равномерно распределенной на отрезке [0, 1].

Поэтому

Умение моделировать непрерывные СВ x дает возможность моделировать любой поток вызовов, заданный последовательностью функций распределения промежутков между вызовами.

В частности, при моделировании простейшего потока вызовов, последовательность случайных величин Zi (промежутки между вызовами) можно получить используя преобразование (9.3).

Дата добавления: 2014-01-11