Основы моделирования коммутационных систем

При моделировании процесса обслуживания входящего потока вызовов КС нет необходимости полностью имитировать реальный процесс. Достаточно ограничиться моделированием некоторого искусственного процесса при условии, что получаемые при этом характеристики в статистическом смысле соответствовали реальному процессу.

Ранее было показано, что обслуживание потока с простым последованием любой КС является марковским процессом. Поэтому вместо моделирования реального процесса можно моделировать марковский процесс.

При этом требуется учитывать случайные отрезки времени пребывания системы в различных состояниях. Дальнейшее упрощение моделирования достигается заменой моделирования марковского процесса моделированием цепи Маркова. При этом переход модели из одного состояния в другое происходит в дискретные моменты времени, в каждый из которых реализация СВ имитирует либо поступление нового вызова, либо окончание обслуживания.

При моделировании цепи Маркова каждое изменение происходит за один цикл работы ЭВМ, в течении которого реализуется случайная величина и происходит переход цепи в другое состояние. Отметим, что при этом не требуется в явном виде учитывать время пребывания системы в различных состояниях.

На рис. 9.3 показана КС произвольной структуры, которая имеет 3 группы входов и h групп выходов.

На каждую группу входов поступает поток с простым последованием с параметром l(i, j, k),

где: i – номер группы входов;

j – номер выбираемого направления

к – номер состояния КС в момент поступления вызова

Обозначим параметр потока освобождений между i – ой группой входов и j – м направлением выходов при котором состояние системы - n(I, j, k). Тогда суммарный параметр потока вызовов ак и суммарный параметр потока освобождений bк в промежутке времени, в которые КС находится в состоянии К, составит:

В каждом состоянии цепи Маркова моделируется СВ x, равномерно распределенная на отрезке [0, ак + bк). Если в рассматриваемом цикле работы ЭВМ СВ x реализуется на участке равномерно распределенного отрезка [0, ак + bк), соответствующем

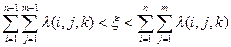
то считается, что эта СВ определяет поступление вызова на n – ю группу входов и соединение требуется установить в требуемом направлении (m).

Если x реализуется на участке

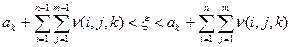
то считается, что соединительный путь между n – ой группой выходов m – й группой входов освобождается.

Дата добавления: 2014-01-11