Переходная функция

Для того, чтобы оценить динамические свойства автоматической системы, следует решить дифференциальное уравнение системы и проанализировать найденное решение. Но решение одного и того же уравнения будет различным при различных формах входного воздействия. Поэтому вначале необходимо решить, какую форму входного воздействия целесообразно выбрать.

Во-первых, воздействие должно соответствовать наиболее тяжелому режиму работы системы из числа встречающихся при ее эксплуатации. Во-вторых, оно должно быть достаточно простым, чтобы не затруднять решения дифференциального уравнения. Этим условиям удовлетворяет единичная ступенчатая функция. Поэтому в теории автоматического управления для оценки динамических свойств систем применяют переходную функцию как реакцию системы на единичную ступенчатую функцию.

Переходная функция – это зависимость изменения выходной координаты от времени, вызванного единичным ступенчатым изменением входной координаты при условии, что до момента приложения этого воздействия система находилась в состоянии покоя.

Графическое изображение реакции системы на единичное ступенчатое возмущение называется переходной характеристикой.

Из определения переходной функции следует, что для ее нахождения необходимо решить дифференциальное уравнение системы (или звена) при 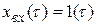при нулевых начальных условиях.

Почему берут не просто скачок, а единичный? Это делается для того, чтобы однозначно оценивать различные системы, так как на скачки различной интенсивности даже одна и та же система реагирует по-разному. По этой же причине выбираются одинаковые начальные условия (нулевые).

Рассмотрим пример определения переходной функции. Найдем переходную функцию звена, дифференциальное уравнение которого имеет вид:

(2.61)

Переходную функцию найдем, решив заданное уравнение при 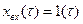и нулевых начальных условиях .

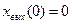Решение этого уравнения состоит из двух составляющих:

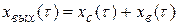(2.62)

где 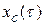– свободное движение системы, которое зависит от свойств самой системы, характеризует переход системы из одного установившегося состояния в другое и представляет собой общее решение однородного дифференциального уравнения;

– вынужденное движение системы, которое зависит от свойств системы и вида входного воздействия, характеризует установившееся состояние и представляет собой частное решение дифференциального уравнения.

Вынужденную составляющую находим из уравнения:

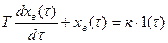(2.63)

Решение уравнения находим при :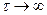

(2.64)

Свободную составляющую находим из уравнения:

(2.65)

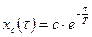(2.66)

Полное решение:

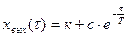(2.67)

Постоянную интегрирования 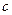находим, воспользовавшись начальными условиями:

с+к=0; с= -к

Окончательно получим:

(2.68)

Это же решение можно получить, воспользовавшись преобразованием Лапласа. Из таблиц преобразований находим:

(2.69)

Тогда

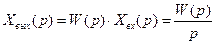(2.70)

Изображение переходной функции равно передаточной функции, деленной на 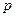. Передаточная функция для данного элемента имеет вид:

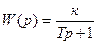(2.71)

Изображение переходной функции

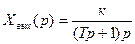(2.72)

Для того чтобы прийти к табличным выражениям, полученное изображение переходной функции запишем в виде суммы простых дробей:

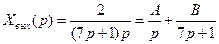(2.73)

Найдем неизвестные коэффициенты :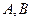

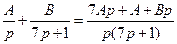(2.74)

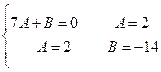(2.75)

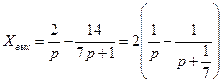(2.76)

Пользуясь таблицами преобразований, находим 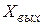(τ) во временной области:

(2.77)

Более наглядное представление о функции дают графики (рис. 2.15).

Рисунок 2.15 – Переходная характеристика элемента системы

Таким образом, рассмотренные характеристики однозначно связаны между собой и, следовательно, одинаково полно определяют динамические свойства систем и их звеньев.

Дата добавления: 2014-01-11