Объектов управления

Экспериментальное определение частотных характеристик

При экспериментальном определении частотных характеристик объектов управления на его вход подают возмущающее воздействие в виде гармонических колебаний, т. е. входную координату изменяют по закону синуса:

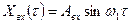(5.46)

Как известно, в этом случае выходная координата также будет изменяться по закону синуса, но выходные колебания будут иметь другую амплитуду и будут сдвинуты по фазе относительно входных колебаний:

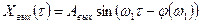(5.47)

Обработка гармонических колебаний не вызывает затруднений. В этом случае непосредственно из графика определяют отношение выходной амплитуды к входной амплитуде

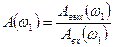(5.48)

и разность фаз между выходными и входными колебаниями

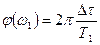(5.49)

Затем подают колебания с частотой ω_2, ω₃ и так далее и определяют 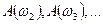, а также 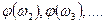По полученным данным строят АЧХ, ФЧХ и АФХ.

Но таким образом в реальных условиях эксперимент не проводят, так как для подачи гармонических колебаний на вход объекта необходимо иметь генератор синусоидальных колебаний, частоту которых можно менять.

Поэтому на практике на вход объекта подают периодические колебания прямоугольной волны (рис. 5.24, а), треугольной волны (рис. 5.24, б) или трапецеидальной волны (рис. 5.24, в).

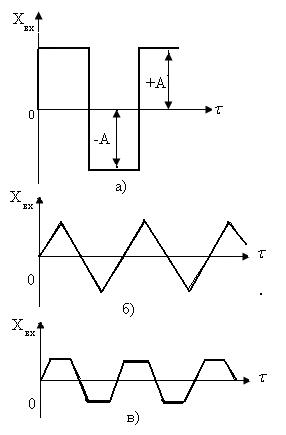
Рисунок 5.24 – Виды входных возмущений при определении частотных характеристик

На практике чаще всего используют входное воздействие в виде прямоугольной волны (рис. 5.24, а). Значение входной координаты изменяют периодически с периодом Т₁=2π/ω₁ и скачкообразно как при определении кривой разгона. При этом периодические возмущения подают достаточно долго, чтобы на выходе объекта установился колебательный процесс, который будет иметь довольно сложную форму (рис. 5.25).

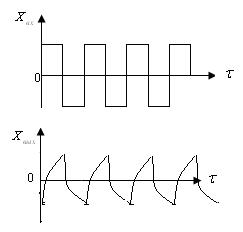
Рисунок 5.25 – Экспериментальные кривые при периодическом воздействии

Для того чтобы обработать полученные кривые необходимо входные и выходные периодические колебания разложить в ряд Фурье. Ряд Фурье для периодической функции записывается следующим образом:

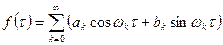(5.50)

где коэффициенты а_к и в_к определяются равенствами:

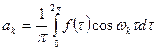(5.51)

(5.52)

Колебания прямоугольной волны можно представить в виде разложения

(5.53)

В этом разложении отсутствуют четные гармоники и коэффициенты а_к равны нулю.

Первая гармоника этого разложения, равная и представляющая собой входную координату, естественно, недостаточно точно описывает входные колебания. К ней можно прибавить третью, пятую и так далее гармоники. Но этого не следует делать, так как выходные колебания также можно разложить в ряд Фурье и из этого разложения выделить только первую гармонику:

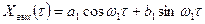(5.54)

Почему это возможно? Потому что и входные и выходные колебания представляют собой сумму гармоник при к, стремящимся к бесконечности. При этом амплитуды последующих гармоник быстро уменьшаются, а частота возрастает. Так как реальные объекты управления плохо пропускают колебания с большой частотой, т.е. являются фильтрами при больших частотах, можно на выходе и на входе использовать только первые гармоники и использовать их для определения частотных характеристик.

Амплитуда первой гармоники входных колебаний определяется по формуле:

А_вх=1,27а,

где а – отклонение входной координаты от среднего значения.

Для разложения выходных колебаний в ряд Фурье пользуются методом шести, двенадцати или двадцати четырех ординат. Для этого отрезок кривой, равный по времени одному периоду (рис 5.26), разбивают в зависимости от выбранного метода на n -интервалов (например, шесть) и определяют ординаты х₀, х₁, х_2, х₃, х₄, х₅, х₆.

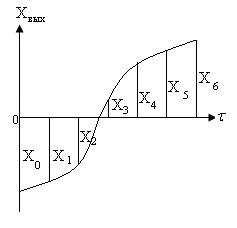
Рисунок 5.26 – К определению синусных и косинусных коэффициентов

Так как х₀=х₆, то рассматривают только ординаты от х₀ до х₅. Имея эти ординаты определяют коэффициенты при косинусе и синусе по формулам:

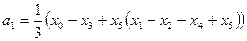(5.55)

(5.56)

После этого определяют амплитуду по формуле:

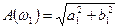(5.57)

А сдвиг фаз первой гармоники по отношению к анализируемой кривой выходных колебаний определяют по формуле:

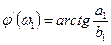(5.58)

Затем непосредственно по графику определяют сдвиг фаз между рассмотренным участком выходных колебаний и колебаниями на входе:

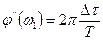(5.59)

Тогда сдвиг фаз выходных колебаний относительно входных колебаний составит:

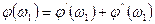(5.60)

Подавая колебания с различными частотами определяют ряд значений А(ω) и φ(ω) и по полученным данным строят АЧХ, ФЧХ и АФХ.

Дата добавления: 2014-01-11