Вычисление ПВИ-1 свидением к ДВИ

Теорема 9.2. (о сведении ПВИ-1 к ДВИ)

Вычисление ПВИ-1 от функции F(x,y,z) по поверхности S, задаваемой уравнением z=f(x,y) сводится к вычислению ДВИ по области S_xy- проекции поверхности S на плоскость xOy. По формуле:

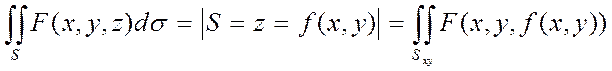
и умножаем на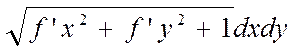(3)

Вывод: для сведения ПВИ-1 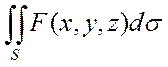, где S:z=f(x,y) к ДВИ по S_xy нужно в подынтегральную функцию F(x,y,z) подставить вместо z f(x,y), а элемент площади поверх ds заменить на .

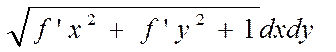Замечание! Если поверхность S задается уравнением y=y(x,z) или x=j(y,z), то аналогично получаем формулы для вычисления ПВИ-1:

1) S:y=y(x,z)=>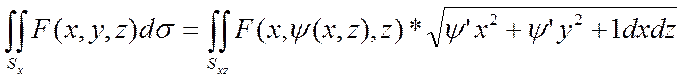 (4)

2)S:x=j(y,z)=>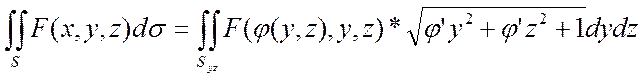 (5)

Л.10. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ по КООРДИНАТАМ (ПВИ-2)

10.1. Классификация гладких поверхностей.

Выберем на гладкой пов-ти S произвольную точку M. Проведём в ней нормаль к пов-ти и выберем конкретное направление вектора нормали (одно из двух возможных).

Опр1. Гладкая пов-ть S наз. двусторонней если при перемещении точки M по произвольному замкнутому контуру, который лежит на этой пов–ти и не пересекает её границу, после этого обхода в направлении нормали не меняется на противоположное.

Опр2. Совокупность всех точек пов-ти S для которых выполняется условие двусторонности (выполняется опр1) наз-ся стороной поверхности

Опр3. Гладкая пов-ть S наз. односторонней, если на этой пов-ти можно указать хотя бы один замкнутый контур не пересекающей границы этой пов-ти при обходе которого направление нормали меняется на противоположное. Примерами двухсторонних пов-тей явл.: плоскость, сфера, эллипсоид, а также любая пов-ть задающаяся ур-ем z=f(x,y), где f(x,y), f^’_x(x,y), f^’_y(x,y) непрерывны в некоторой обл. S_xy – проекции S на пл. xOy. Примером односторонней пов-ти явл. Так называемый лист Мебиуса.

Опр4. Двусторонние пов-ти наз. ориентированными пов-тями, а выбор стороны пов-ти(определённый) наз. её ориентированными.

Опр5. если определённая сторона пов-ти выбрана(пов-ть сориентирована) то за положительное направление обхода замкнутого контура, расположенного на пов-ти S, считается то, при котором для наблюдателя, расположенного в конце вектора нормали обход этого контура осуществляется против часовой стрелки(противоположное направление обхода) наз. отрицательным.

Если изменить ориентацию пов-ти на противоположную, то положительное и отрицательное направления обхода меняются местами.

10.2. ПВИ-2: определение, теорема существования.

Пусть S гладкая двусторонняя пов-ть определяемая ур-ем z=f(x,y), ограниченная замкнутой линией L в точках которой определена функция трёх переменных R=R(x,y,z). Выберем определённую сторону этой пов-ти.

Выполняем следующие стандартные действия:

1)Разобьем пов-ть S на n частичных пов-ей d_I =(i=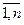) l - диаметр разбиения

2)Выберем произвольную т. M_i (x_i, y_i, z_i)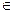d_I и составляем сумму:

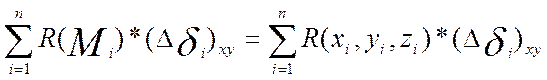(1)

где 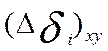- площадь проекции i-й элементарной площадки d_i на пл. xOy, взятая со знаком «+», если выбранная внешняя сторона пов-ти или что тоже самое угол между вектором нормали к этой пл-ти и осью O_z – острый 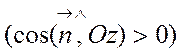; и взятая со знаком «-» если выбранная нижняя сторона пов-ти, т.е. угол между вектором нормали и осью Oz – тупой.

Если существует конечный предел интегральной суммы (1) при 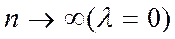, то он наз. поверхностным интегралом по выбраной стороне S от функции R(x, y, z) по координатам(переменным) x и y и обозначается

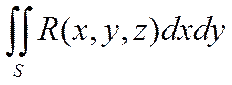(2)

Таким образом (2)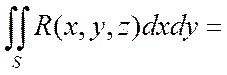

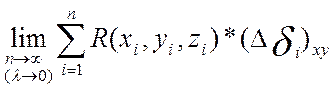
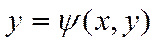
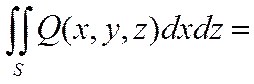
Аналогично определяется ПВИ-2 по координатам x и z от функции Q=Q(x, y, z), если пов-ть S задана ур-ем 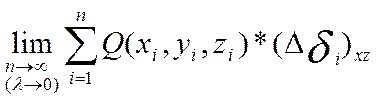(3)

А также ПВИ-2 по координатам y и z от функции P=P(x, y, z), если S: x=j(x, y)

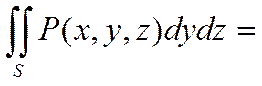
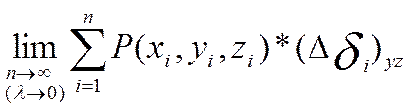(4)

если во всех точках пов-ти S опрделены все 3 функции P, Q, R и существуют интегралы (2), (3), (4); то сумма этих интегралов наз. ПВИ-2 общего вида т.е. 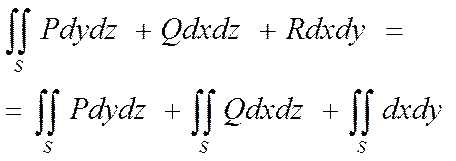(5)

Дата добавления: 2014-01-11