Потенциальное (безвихревое) ВП и его свойства

Опр 5. ВП называется потенциальным (безвихревым) если в каждой точке этого поля ротор поля равен 0.

Основные свойства потенциального поля:

1.потенциальное поле является полем grad некоторого СП u=u(x,y,z)

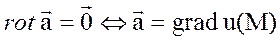
Докажем достаточность этого свойства:

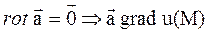
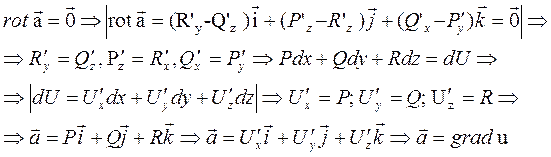
Докажем необходимость :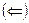

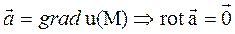
2.циркуляция потенциального поля по любому замкнутому контуру в потенциальном поле равна 0: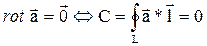

Доказательство этого свойства следует из формулы Стокса, т.е.

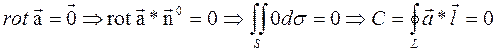
3.в потенциальном поле линейный интеграл 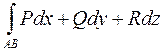поля не зависит от формы пути интегрирования, а его значение определяется разностью значений потенциала поля в точке В и в точке А

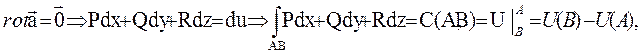
где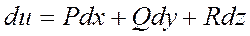

Опр 6. Функция U называется скалярным потенциалом или потенциальной функцией поля .

Потенциал поля u=u(x,y,z) восстанавливается по ее полному дифференциалу 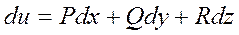по формуле:

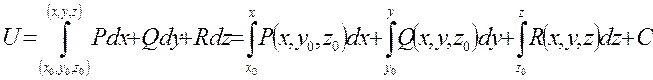
14.5 Гармоническое поле

Опр 7. ВП наз. гармоническим, если оно одновременно и соленоидальное 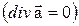и потенциальное .

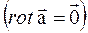Т.к. поле является потенциальным, то его можно записать в виде 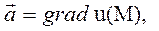а так как оно и соленоидально, то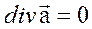

Тогда

В развернутом виде: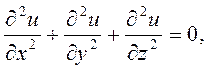

где u - потенциал поля.

Следовательно, потенциал поля u, если это поле гармоническое является решением дифференциального уравнения 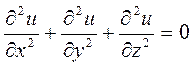в частных производных, которые называются дифференциальным уравнением Лапласа.

Всякое решение уравнения Лапласа называется гармонической функцией.

Л.15 ЭЛЕМЕНТЫ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. Комплексные числа(к/ч).

15.1. К/ч определение, геометрическое изображение.

Опр.1. Результат извлечения корня квадратного из отрицательного числа назыв. мнимым числом.

Если d>0, то √-d = √d * (-1) = ±√d * √-1 (1)

Опр.2. Мнимое число √-1 назыв. мнимой единицей и обозначается i, т.е. i=√-1.

Отсюда следует, что i² = -1; i³ =i² * i = -1√-1=-1i; i⁴ = i² * i² = -1* (-1)=1;

(i⁴ⁿ)=(i⁴)ⁿ = 1

Например i²³ = (i⁴)⁵ * i³ = i³ = -i.

Вывод: на основание выше написанной формулы любое мнимое число можна представить в виде произведения действительного числа на мнимую единицу.

Опр.3. Комплексным числом z называется соединение действительного числа a с мнимым числом bi (a,b€R) с помощью знака “+”. Иными словами комплексным числом z называется выражение вида z= a + bi. При этом a – действительная часть комплексного числа z(a=R€z), а число b – мнимая часть к/ч и обознач. b = I_mz.

Если b=0, то z=a – действительное число.

Если a=0, то z=bi – мнимое число.

Если a=0 и b=0, то z= 0+0*i=0

Из этого следует, что действительные числа и мнимые являются частными случаями множества к/ч.

Опр.4. Число z=a-bi называется сопряженным к/ч z=a+bi и наоборот, два комп. числа z и z являются (взаимно) сопряженными тогда и только тогда когда они отличаются знаком мнимой части равны:

z₁=a₁+b₁i <=> a₁=a₂

z₂=a₂+b₂i <=> b₁=b₂

15.2 Геометрическое представление к/ч.

b M(a,b)

	|z|=ρ

a

|z|=√a² +b² a=ρcosφ

b=ρsinφ

φ=argz= argz +2Пk, k€z

Тригонометрическая форма к/ч: z= ρ(cosφ+isinφ)=|z|(cos(argz)+isin(argz))

Формула Эйлера: e^iφ =cosφ+isinφ

z= ρe^iφ= |z|e^iargz

    Arg z=

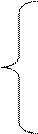arctg b/a, a>0

П + arctg b/a, a<0, b>0

П + arctg b/a, a<0, b<0

П/2, a=0, b>0

-П/2, a=0, b<0

пример:

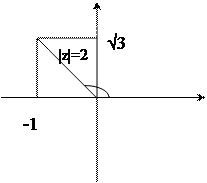
z=-1+√3i

R_ez =-1

I_mz=√3

|z|=ρ=√(-1)² + (√3)² = √4 =2;

arg z= П+ arctg (√3/-1)=П-arctg√3 = П – П/3= 2П/3;

z= 2(cos 2П/3 +isin 2П/3);

z= 2e ^i2П/3

15.3 Операция над к/ч.

1) Сложение и вычитание:

z₁=a₁+ib₁

=> z₁±z₂ => (a₁±a₂)+ i(b_i±b₂)

z₂=a₂+ib₂

пример:

z₁=-1+5i => z₁+z₂ = (-1+4)+ i(5-8)=3-3i

z₂=4-8i z₁-z₂ = (-1-4)+ i(5+8)= -5+13i

Тригонометрическая форма:

z₁=ρ₁(cosφ_1­+isinφ₁)

=>z₁±z₂=(ρ₁cos φ₁± ρ₂cosφ₂)+ i (ρ₁sinφ₁± ρ₂sinφ₂)

z₂=ρ₂(cosφ₂+isinφ₂)

пример:

z₁=e²ⁱ => z₁=cos2 + isin2

z₂=3e^-i z₂=3cos1-isin1

2) Умножение и деление

z₁=a₁+b₁i

=> z₁*z₂ =(a₁+ib_i)(a₂+ib₂)=a₁a₂+ib_ia₂+ib₂a₁+i²b₁b₂= (a₁*a₂-b₁*b₂)+i(a₂b₁+a₁b₂)

z₂=a₂+b₂i

z=z₁*z₂ Rez=a₁a₂-b₁b₂

Imz=a₂b₁+a₁b₂

Тригонометрическая форма:

z₁=ρ₁(cosφ₁+isinφ₁)

z₂=ρ₂(cosφ₂+isinφ₂)

Rez₁=ρ₁cosφ₁ Imz₁=ρ₁sinφ₁

Rez₂=ρ₂cosφ₂ Imz₂=ρ₂sinφ₂

z=z_1*z₂

Rez= ρ₁cosφ₁* ρ₂cosφ₂ - ρ₁sinφ₁* ρ₂sinφ₂= ρ₁ρ₂(cosφ₁cosφ₂ - sinφ₁sinφ₂)= ρ₁ρ₂ cos(φ₁φ₂)

Imz= ρ₂cosφ₂* ρ₁sinφ₁ + ρ₁cosφ₁* ρ₂sinφ₂= ρ₁ρ₂(cosφ₂sinφ₁ + cosφ₁sinφ₂)= ρ₁ρ₂ sin(φ₁φ₂)

Итак, z₁z₂= ρ₁ρ₂ (cos(φ₁φ₂)+ isin(φ₁φ₂))

Возведение к/ч в степень:

zⁿ=(a+ib)ⁿ

z= ρ(cosφ+isinφ) => z²=z*z = ρ²(cos2φ+isin2φ)

z³=z²*z = ρ³(cos3φ+isin3φ)

zⁿ=ρⁿ(cosnφ+isinnφ)- формула Муавра

z=ρe^iφ => zⁿ= ρⁿe^inφ

Извлечение корня n-ой степени из к/ч

z= ρ(cosφ+isinφ)

ⁿ√z =w, z=wⁿ

w=r(cost+isint), r,t-?

ρ(cosφ+isinφ)= rⁿ(cos nt+isin nt)

ρ=rⁿ r=ⁿ√ρ

φ+2Пk=nt t=φ=2Пk/n, k=0,1,….,n-1

ⁿ√z = ⁿ√ρ (cos 2Пk/n + isin 2Пk/n)

Деление к/ч

Опр.6 Частным двух к/ч z₁ и z₂ называется к/ч z, вычисляемое по формуле: z=a+bi =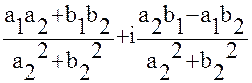

На практике деление двух к/ч осуществляют след образом:

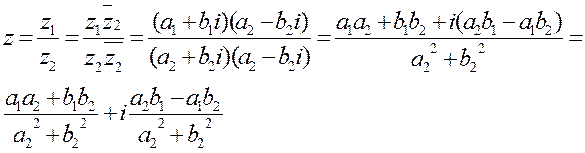
z = z₁/z₂ = ρ₁(cosφ₁+isinφ₁)/ ρ₂(cosφ₂+isinφ₂)= ρ₁ /ρ₂ (cos(φ₁-φ₂)+ isin(φ₁-φ₂))

Деление к/ч в показательной форме:

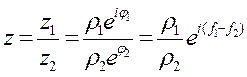
Дата добавления: 2014-01-11