Понятие расширенной комплексной z-пл

При выполнение деления чисел z₁ и z₂ предполагалось что z₂≠0, т.к в противном случае если z₂=0, то деление невозможно.

Для устранения этого договоримся что на множестве к/ч, частное 1/0 существует и представляет собой число, которое обозначают символом «∞».

Опр 7. Число z=∞ равное 1/0 называется несобственным (бесконечным к/ч). Множество к/ч С дополненное числом z =∞ называется расширенным множеством к/ч.

Комплексное пл. z, дополненная точкой z=∞ называется расширенной комплексной плоскостью. А сама т. z=∞ называется ее бесконечно удаленной точкой. Для числа z=∞ не сущ. понятия действительной и мнимой части, а также аргумента. Модуль этого числа |z|=±∞.

Л.16 ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ. Функция комплексного переменного (ФКП) и её приделы.

16.1. Последовательность комплексных чисел определение, критерий существования.

Пусть {a_n}, {b_n} – последовательность действительных чисел. Каждой упорядоченной паре: (a_n, b_n) поставим в соответствие комплексное число z_n = a_n+ b_ni.

Опр1. Множество комплексных чисел {z_n} (n € N), таких что Rez_n = a_n, Imz_n= b_n, расположэных в порядке возростания их номеров, называется последовательностю комплексных чисел.

Последовательность комплексных чисел щитается заданной, если извесна формула его общего члена, при этом a_n и b_n – действительные функции натурального аргумента n.

Опр2. Число с € С – называется приделом последовательности комплексных чисел, если для любого έ >0 существует такой номер n₀ € N, зависящий от έ, что при всех n>=n ₀ выполняется неравенство:

|z_n-c|< έ.

Опр3. Круг на комплексной плоскости z, с центром в точке с и радиусом έ, называется έ-окресностю точки с, и обозначается U_έ(c).

U_έ(c)↔{z €С| |z-c |<έ}.

С геометрической точки зрения Опред2 можно интерпретировать следующим образом: если число с является приделом последовательности комплексных чисел, то для любой έ-окресности точки с, существует такой номер n ₀€ N, начиная с которого все члены последовательности {z_n} попадут в έ-последовательность точки с.

Опр4. Если {z_n} имеет конечный придел, то она называется сходящейся, в противном случае{z_n} называется расходящейся, и её приделом является бесконечно удалённая точка z=∞.

Теорема 16.1 (Критерий сходимости).

Для того, что бы последовательность комплексных чисел была сходящейся, необходимо, чтобы отюельно сходилась последовательность {a_n} и {b_n}.

(lim z_n =lim (a_n + b_ni)=c= a_c b_ci↔ lim a_n = a_c∩ lim b_n=b_c).

^{n->∞ n->∞ n->∞ n->∞}

Сформулированная теорема позволяет распостранить теорию приделов последовательностей действительных чисел, на последовательность комплексных чисел.

16.2 Арифметические свойства приделов комплексных чисел.

Пусть {z_n} и {z’_n} – сходящиеся комплексные числа

1. lim z_n (k₁z₁± k₂z₂)= k₁ lim z_n± k₂lim z₂, где (k_1,k₂ --const)

^{n->∞ n->∞ n->∞}

2.lim (z₁ z₂ )= lim z₁ * lim z₂

^{n->∞ n->∞ n->∞}

3. lim z₁/z₂ = lim z₁ / lim z₂

^{n->∞ n->∞ n->∞}

Пример: Найти придел последовательности комплексных чисел:

z_n =1/3ⁿ+I (2n+5)/(6n+1)

a_n=1/3ⁿ ; b_n=(2n+5)/(6n+1)

lim a_n= lim 1/3ⁿ=0;

^{n->∞ n->∞}

lim b_n= lim(2n+5)/(6n+1)= 1/3

^{n->∞ n->∞}

Ответ: lim z_n=0+1/3i=1/3i

16.3 Функция комплексного переменного: определение, непрерывность.

Пусть x и y – некоторые действительные переменные, тогда выражение z=x+iy называется комплексной переменной.

Обозначим Д_z – множыство всех значений, которая может принимать комплексная переменная z.

Оперед5. Если каждому значению z€Д_z по определённому правилу или закону f ставится в соответствие w=f(z) € С, то говорят, что на множестве Д_z задана однозначная функция комплексного переменного w=f(z). если каждому z соответствует несколько функций w=f(z) – она называется многозначная функция комплексного переменного.

Опред 6. Множество Д_z называется областю определения (существования) ФКП w=f(z), а множесво Д_w – всех значений которые принимает f(z), на множестве Д_z, называется областю значений существования функции w=f(z).

Всякую ФКП можно записать w=f(z)=f(x+iy)=U(x,y)+iV(x,y), где U=U(x,y) – называется действительной частью ФКП, а V – мнимой частю.

U(x,y)=Rew

V(x,y)=Imw

Вывод: задание ФКП как однозначной так и многозначной, равносильно заданию двух действительных функций U и V, двух действительных переменных.

Пример:

Найти Rew, Imw функции w=z²

w=z²=(x+iy) ²= x²+2ixy+i²y²= x²+2ixy-y²= x²-y²+2ixy

Rew= x²-y²

Imw=2xy

Опр.7 Функция w=f(z), для любого z€Д_z, называется непрерывной в точке z=z₀, если придел функции в этой точке равен значению функции в этой точке. Функция называется непрерывной в области Д, если она непрерывна в каждой точке этой области.

Л.17 Основные элементарные ф.-ции комплексного переменного (ФКП)

17.1. Однозначные элементарные ФКП.

К основным однозначным ФКП ω=f(Z) относятся:

-степенная ω=Zⁿ (nєN);

-показательная e^z;

-тригонометрическая sin Z,cos Z,tg Z, ctg Z и гиперболические ф.-ции sh Z, ch Z, th Z, ctg Z.

17.1.1. Степенная ф.-ция: ω=Zⁿ.

Если nєN, то ω=Zⁿ, наз. ФКП определяемой формулой Zⁿ=ρⁿ (cos nφ+isin nφ) – (1)

17.1.2. Показательная ф.-ция: ω=e^z

Показательной наз.- ФКП определенная формулой ω=e^z =e^x+iy=e^x(cosy+isiny) - (2)

Если I_mz=y=o, т.е. Z=x+i0=x –действительно, то E^z – показательная ф.-ция действ. переменного e^x.

ω= e^z(Zє C )св.-ва:

1) e^z1e^z2=e^{x1 iy1} e^{x2 y2} = | (Z)…| =e^x1(cos y₁+isiny₁)* e^x2(cos_y2+isin_y2)=e^x1+x2(cos(y₁+y₂)+isin(y₁+y₂)=e^{(x1+x2)+i(y1+y2)}=e^z1+z2

2) (e^z)ⁿ=e^zn, (nєZ)]

3) |e^z|=|e^x(cosy+isiny)|=√(e^xcosy)²+(e^xsiny)²=e^x√cos²y+sin²y=e^x≠0

4) e^z1:e^z2=e^z1-z2

5) e^z+2πi=e^z*e^2πi=e^z(cos2π+isin2π)=e^z

Вывод: ф.-ция ω=e^z периодична с периодом 2πi

17.1.3. Тригонометрические ф.-ции.

Связь между показательной и тригонометрическими ф.-циями устанавливает ф.-ла Эйлера.

E^iz=cosz+isinz - (3)

Подставим вместо Z(-Z): e^-iz=cos(-Z)+isin(-Z)=cosZ-isinZ - (4)

| (3) + (4) ……|= cosZ=e^iz+e^-iz/Z - (5)

| (3) - (4) …… |= sinZ=e^iz-e^-iz/2i - (6)

tg Z=sinZ/cosZ Z≠π/2 +2πk - (7)

ctgZ =cosZ/sinZ Z≠πk, kєZ - (8)

Замечание: ф.-ции sinZ и cosZ в комплексной плоскости Z не ограничены:

Lim sinZ=∞

z->±∞

Lim cosZ=∞

z->±∞

17.1.4. Гиперболические ф.-ции (shZ, chZ, thZ, cthZ)

Гиперболическими наз. ФКП определяемые ф.-ами:

shZ=e^z-e^-z/Z -(10)

chZ=e^Z+e^-Z/Z - (11)

tgZ= shZ/chZ -(12)

ctgZ=chZ/shZ -(13)

Заменяя в ф.-лах (9)-(13) Z на iZ получаем ф.-лы, связывающие гиперболические и тригонометрические ф.-лы:

sh iZ =i sinZ

sh Z=-I sinZ

ch iZ =cosZ

chZ= coz iZ (14)

th iZ=shZ/chi Z=i tgZ

thZ =-i tg iZ

cth iZ=chZ/shi Z=-i ctgZ

cthZ=i ctg iZ

Пользуясь ф.-ами (14) можно получить ряд ф.-ул., связывающих тригонометрические ф.-лы:

1) cos²z+sin²z=ch iZ+shi Z/i=ch iZ-sh iZ=1

2) ch2Z=ch²Z+sh2Z

3) sh2z=2shZ *chZ

4) sh(-Z)=-shZ

5) ch(-Z)=chZ

shZ и сhZ периодические с периодом 2πi.

17.2. Многозначные ФКП.

Многозначные ФКП как правило явл. обратными к рассмотренным однозначным ФКП или явл. их обобщениями.

17.2.1. Логарифмическая ф.-ция

Логарифмическая ф.-ция ω=LnZ, где Z≠0, определяется как ф.-ция обратная показательной.

По определению логарифмом числа “Z” наз. Такое число “ω”, что e^ω =Z.

Как было показано в п. 17.1.2., показательная ф.-ция е^ω=Z≠0, следовательно ω=LnZ определена на всей Z- плоскости за исключением точки Z=0.

Найдем выражение для ω:

e^ω= Z=> ω=U+iU => U=lnρ=ln |Z| => ω=ln|Z|+i ArgZ

Z=ρ e^iφ V=argZ

=ln|Z|+i (argZ+2πk)

ω=LnZ=ln|Z|+i(argZ+2πk) - (16)

Логарифмическая ф.-ция φ=LnZ обладает следующими св.-вами:

1) Ln (Z₁+Z₂)=LnZ₁+Lnz₂

2) Ln(Z₁-Z₂)=LnZ₁-LnZ₂

3) Ln (Zⁿ)=n LnZ

4) Ln(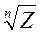)=1/n LnZ

17.2.2. По определению arcsin числа Z наз. число ω,

такое что sin ω=z и обозначается Arcsin Z

ω=Arcsin Z

Z=sin ω=>Z=e^iω-e^-iω/2i=>2iz=e^iω-1/e^iω=>e^2iω-2ize^iω-1=0

Пусть e^iω=t≠0

T²-2iZt-1=0

D=(-2iZ)²-4*1*(-1)=-4Z²+4

t_1,2=2iZ+=iz+

e^iw=iZ+;

iω=Ln(iZ+);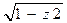

ω=1/nLn (iZ+);

Arcsin Z=-iLn(iZ+);

Arccos Z=-i Ln (Z+);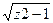

Arctg Z=- i/2 Ln i-Z/Z+1

Замечание: т.к. обратные тригонометрические формулы выражаются через Ln Z,то они явл. многозначными.

17.2.3. Обобщенная степенная показательная ф.-ция

Ф.-ция ω=Z₀, где a=α+iβ- некоторое комплексное число, определяемое ф.-лой ω=e^alnZ(где Z≠0)-наз. Обобщенной степенной ф.-цией, а ω=e^alnZ-её главное значение.

Ф.-ция ω=a^z,где Zє C, определяемая ф.-лой:

ω=Z^a, где a=α+iß

ω=e^aLnZ (Z≠0) -обобщенная степенная ф.-ция

а ф.-ция ω=e^aLnz- наз. главным значением ф.-ции.

Дата добавления: 2014-01-11