Интегрирование дробно-рациональных функций

Пусть требуется найти неопределенный интеграл вида, где

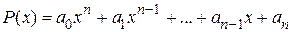и .

Если степень n многочлена, стоящего в числителе, больше степени m, многочлена, стоящего в знаменателе, т. е. 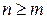, то необходимо в первую очередь выделить целую часть. Для этого можно использовать деление уголочком.

Например, пусть имеется неправильная дробь 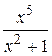. Делим и получаем

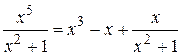
Если дробь 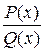правильная, т. е. 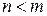, то многочлен 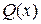, стоящий в знаменателе, нужно разложить на множители вида 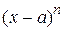и ,

где m и n степени кратности множителей. Здесь предполагается, что квадратный трехчлен 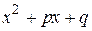не имеет вещественных корней. При разложении дроби 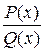на сумму простых дробей каждому множителю будет соответствовать столько слагаемых, какова его степень. Например,

.

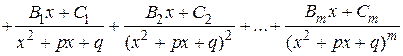Для того чтобы найти постоянные коэффициенты

в данном разложении, необходимо сумму дробей привести к общему знаменателю и приравнять многочлены, стоящие в числителях левой и правой частей. Для нахождения коэффициентов составляется система линейных уравнений. При этом возможно использовать два способа. В одном из них приравниваются коэффициенты при одинаковых степенях переменной х в многочленах левой и правой частей. В другом способе приравниваются значения многочленов при каких-либо специально выбранных значениях х. Возможно также совместное применение этих способов.

Пример 4.25. Найти интеграл .

Разложим подынтегральную функцию на простые дроби

.

Приведем сумму простых дробей к общему знаменателю

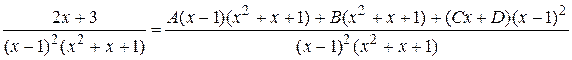
Приравниваем числители дробей

.

.

Приравниваем коэффициенты при одинаковых степенях х многочленов левой и правой частей, получаем систему и решаем ее.

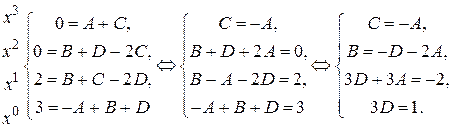
Получаем решение системы

, .

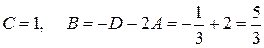Находим интеграл

.

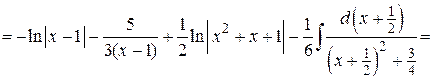
Пример 4.26. Найти интеграл .

Разлагаем подынтегральную функцию на простые дроби

.

Приравниваем числители дробей

.

Составляем систему для нахождения неопределенных коэффициентов.

В последнее равенство подставляем различные значения х, получаем

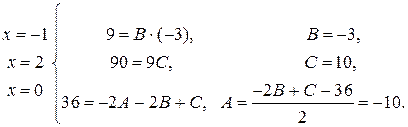
Находим интеграл

.

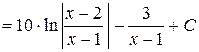Дата добавления: 2014-01-11