Вторичная проекция точки, лежащей в плоскости картины П/ (точка М), находится на основании картины (линии O1 – O2)

Вторичные проекции точек, расположенных в промежуточном пространстве (точка L), находятся ниже основания картины (линии O1 – O2), а расположенных в мнимом пространстве (точка К) – выше линии горизонта.

При удалении точки, находящейся в предметном пространстве, от плоскости картины П/ расстояние от ее вторичной проекции А1/ до основания картины

(линии O₁ – O₂) увеличивается, а вторичные проекции точек находятся между основанием картины (линией O₁ – O₂) и линией горизонта картины h – h (точки А и В).

На основе изложенного материала могут решаться прямые и обратные задачи по построению наглядного изображения (изображение в косоугольной фронтальной диметрической аксонометрической проекции) положения точки в пространстве или ее перспективы и вторичной проекции.

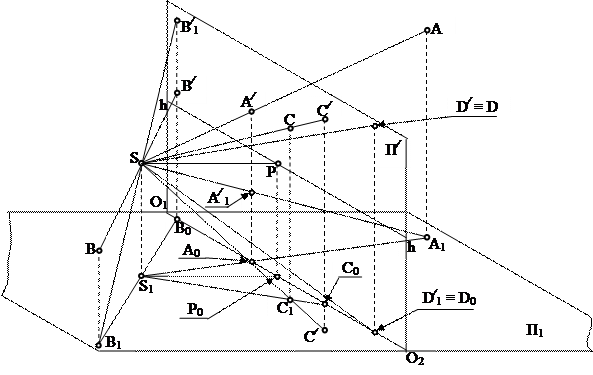
Пример 7. Построить положение точек A, B, C и D в пространстве по заданным их перспективам и вторичным проекциям (прямая задача) и построение перспектив и вторичных проекций по заданному положению точек (обратная задача) (рис. 75).

		Рис. 75. Построение положения точек по заданным их перспективам и вторичным проекциям.

Алгоритм решения задач следующий. Сначала задается положение предметной плоскости П₁ и плоскости картины П^∕, строится линия начала картины(О₁ – О₂). По заданным параметрам высоты горизонта H и главного расстояния d строится положение точки зрения S относительно плоскости картины П^∕ и предметной плоскости П₁. Строятся основание точки зрения S₁, линия горизонта (h - h), главная точка картины P и основание главной точки картины P₀.

- прямая задача (на примере построения точки А) (см. рис. 75).

1. Линия проекционной связи проекций А^∕ и А^∕₁ продлевается в плоскости картины П^∕ до пересечения с линией начала картины (О₁ – О₂) и через полученную точку А₀ и точку стояния S₁ проводимслед лучевой проецирующей плоскости;

2. Через точку зрения S и вторичную проекцию точки А^∕₁ проводится луч до пересечения с продолжением линии (А₀ - S₁): полученная точка пересечения А₁ – это проекция точки А на предметной плоскости;

3. Точка А найдется на пересечении луча (S - А^∕) с вертикальной линией проекционной связи из точки А₁;

- обратная задача (на примере построения точки В) (см. рис. 75).

1. Из точки В опускается вертикальная линия проекционной связи на предметную плоскость П₁ – получаем проекцию точки на предметной плоскости В₁. Проводим след лучевой проецирующей плоскости через точки В₁ и S₁;

2. В точке пересечения линии (В₁ - S₁) с линией начала картины (О₁ – О₂) получаем точку В₀ – проекцию перспективы и вторичной проекции точки В на линии начала картины (О₁ – О₂). Из точки В₀ в плоскости картины П^∕ восстанавливаем вертикальную линию проекционной связи;

3. Перспектива точки В^∕ найдется в точке пересечения вышеуказанной линии проекционной связи с лучом (S - В), а вторичная проекция В^∕₁ - с лучом (S – В₁).

Дата добавления: 2014-01-11