
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аксиоматика функциональных зависимостей Армстронга
|
|
|
|
Аксиомы:
Аксиомы: Пусть R—множество атрибутов, AÍR. Аксиомой является функциональные зависимости вида A®A.
Правила вывода:
1) правило накопления
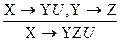
2) правило проективности
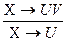
Определение. Пусть F- множество формул над схемой R, X,YÍR. Формула X®Y является логическим следствием набора формул F, если для любого отношения r над схемой R, если все формулы из F выполняются в r, то в r выполняется формула X®Y. Множество всех логических следствий из F будем обозначать F*.
Определение. Пусть F- множество формул над схемой R. Замыканием F (обозначается [F]) называется множество всех формул, выводимых из F.
Определение. Исчисление называется полным, если для любого множества формул F F*Í [F]. Исчисление называется непротиворечивым, если [F] Í F*.
Теорема полноты. Аксиоматика Армстронга является полной и непротиворечивой.
Доказательство. 1. Докажем сначало непротиворечивость. Пусть F – непустое множество формул над схемой R.. Нам надо показать, что любая формула, выводимая из F по правилам Р1, Р5, является логическим слествием. Пусть r- произвольное отношение, в котором выполняются формула X®Y из F, т.е. ("t, qÎr) t(X)=q(X) ® t(Y)=q(Y). Пусть для кортежей t, qÎr выполняется t(XZ)=q(XZ), тогда выполняется и t(X)=q(X), и, значит, t(Y)=q(Y). Это означает, что в r выполняется формула XZ®Y. Значит, формулы, выведенные по правилу Р1, являются логическими следствиями F. Аналогично доказывается, что применение правила P5 также дает логические следствия (доказать самостоятельно!), и первая часть теоремы доказана.
2. Докажем теперь полноту аксиоматики Армстронга. Пусть она – не полна. Тогда существует формула X®Y, являющаяся логическим следствием F, но не выводимая из F. Заметим, что если из F выводимы формулы X®Y, X®Z, то по правилу аддитивности выводима формула X®YZ. Поэтому, найдется некоторое максимальное множество V такое, что X®V выводимо из F, и для любого Z, X®Z выводимо, влечет ZÍV. В силу предположения, Y не содержится в V. Определим некоторое отношение r, содержащее два кортежа:

| 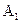
| … | 
|

| … | 
| |
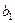
| … | 
|
где 
Очевидно, что p(X)=q(X), и p(Y)¹q(Y), поэтому формула X®Y не выполняется в r. Покажем, однако, что все формулы из F, выполняются в r. Действительно, пусть формула A®B принадлежит [F]. Если A не является подмножеством U, то p(A)¹q(A), и формула p(A)=q(A)® p(В)=q(В) истинна. Если AÍU, то BÍU, т.к. выводимо X®U, U®A, A®B и по правилу транзитивности, X®B, и в силу выбора U, BÍU. Таким образом, все формулы из F выполнимы в r, а формула X®Y не выполняется в r, и, значит, последняя формула не является логическим следствием формул F. Получили противоречие, и теорема доказана.
Доказанная теорема дает практический способ проверки выводимости формулы  из набора
из набора  других формул:
других формул:
1) ищем максимальное  :
: 
2) проверяем: 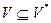 (если ‘да’, то V выводима из U)
(если ‘да’, то V выводима из U)
Пример
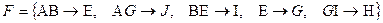
Проверим, выводима ли 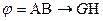 .
.
Рисуем граф:

 J
J


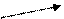
 AB E G
AB E G
 I
I
H
Вывод: замыкание АВ содержит весь перечень формул, то есть 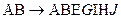 , JH – подмножество этой формулы
, JH – подмножество этой формулы 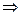 выводимо.
выводимо.
Оценка сложности и построение максимального множества
Исходное множество 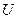 разрастается путем добавления новых элементов.
разрастается путем добавления новых элементов.
Наихудший случай: 
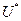 - строится за n шагов
- строится за n шагов 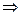
 .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 783; Нарушение авторских прав?; Мы поможем в написании вашей работы!