Структура неизбыточных покрытий

End.

Begin

End.

Begin

v:= ложь

for каждая F-зависимость 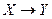из F do

if MEMBER(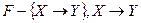) then v:= истина;

return (v)

Для любого множества F-зависимостей G существует некоторое подмножество F, такое, что F является неизбыточным покрытием G. Если G неизбыточно, то F=G. Если G избыточно, то в G существует F-зависимость 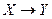, которая является избыточной в G. Пусть 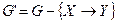. Заметим, что 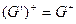. Если G’ избыточно, то в G’ существует избыточная F-зависимость 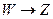. Пусть G’’=G’-{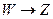}; (G’’)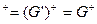. Процесс удаления избыточных F-зависимостей, естественно, должен закончиться. В результате для G образуется неизбыточное покрытие F. Этот процесс является основой алгоритма 5.4 NONREDUN, который для множества F-зависимостей вычисляет неизбыточное покрытие.

Алгоритм 4. NONREDUN

Вход: Множество F-зависимостей G.

Выход: неизбыточное покрытие G.

NONREDUN(G)

F:=G;

for каждая F-зависимость 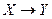из G do

if MEMBER (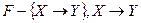) then

F:=F-{};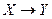

return (F)

Пример 3. Пусть 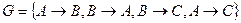. Результатом работы NONREDUN(G) является множество 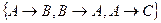. Если G представлено в порядке 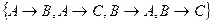, результатом NONREDUN(G) является .

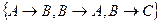Из примера 3 видно, что множество F-зависимостей G может иметь более одного неизбыточного покрытия. Могут также существовать неизбыточные покрытия G, не содержащиеся в G. В примере 3 таким неизбыточным покрытием G служит множество F=.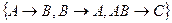

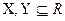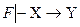Определение Множества называются эквивалентными относительно , если и 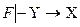(обозначение ).

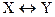Теорема (о структуре неизбыточного покрытия). Если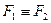-неизбыточные покрытия, то 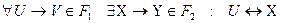относительно .

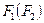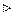Доказательство. 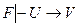. Строим 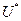и для построения рассмотрим формулы 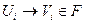. Если 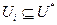тогда . .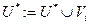

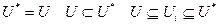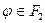Пусть . Рассмотрим вывод над 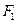. Существует формула 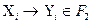:в её выводе используется . Действительно, если бы её не существовало, то каждую формулу из 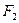можно бы было получить из 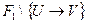, т.к. 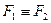, то 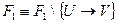, то есть 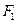- избыточно. Приходим к противоречию.

Пусть в выводе 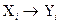используется . Тогда 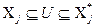. Имеем 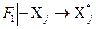, откуда по правилу проекции .

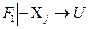Обратно 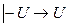- аксиома.

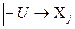, т.к. .



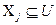Дата добавления: 2014-01-11