Покрытия функциональных зависимостей. Структура неизбыточных покрытий

Рассмотрим некоторые методы представления множеств F-зависимостей. Например, любая F-зависимость, выводимая из множеств 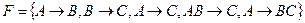, также выводима из множества 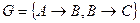, поскольку все F-зависимости из F мо­гут быть выведены из F-зависимостей, принадлежащих G. По какой причине предпочтительнее более короткие представления?

Меньшее множество F-зависимостей гарантирует более быстрое исполнение алгорит­мов. Далее приводятся другие алгоритмы, для которых временная сложность также зависит от числа F-зависимостей на входе.

В системах баз данных F-зависимости способствуют обеспечению согласованности и целостности баз данных. Меньшее число F-зависимостей означает меньший объем исполь­зуемой памяти и меньшее количество проверок при модификации баз данных.

Определение 1. Два множества F-зависимостей F и G над схемой R эквивалентны, 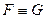, если 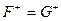. Если 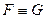, то F есть покрытие G.

В определении для покрытия нет упоминания об относительных размерах F и G. Однако далее рассматриваются покрытия частного вида, в которых F не превосходит G по числу F-зависимостей.

Если 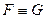, то, поскольку 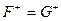, для каждой зависимости 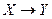из 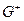следует .

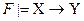В частности, для каждой F-зависимости 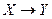из G имеет место 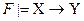. Обобщим понятие выводимости на множество F-зависимостей, записав это условие в виде . Поскольку определение эквивалентности симметрично относительно F и G, из 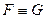сле­дует .

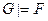Так как 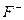включает каждую F-зависимость 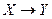, такую, что 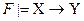, то из следует 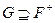. Применяя операцию замыкания к обеим частям неравенства, полу­чаем 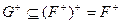. Аналогично 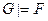влечет за собой 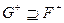. Таким образом, дока­зана

Лемма 1. Для заданных множеств F-зависимостей F и G над схемой R тождество 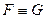имеет место тогда и только тогда, когда и .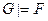

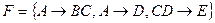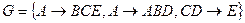Пример 1. Множества и эквивалентны. Множество F не эквивалентно множе­ству G¢ 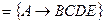, поскольку соотношение G¢ |= CD 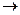E не выполняется.

Лемма 1 содержит простой способ проверки эквивалентности двух множеств F-зави­симостей. Функция DERIVES проверяет условие .

Алгоритм 1. DERIVES

Вход: два множества F-зависимостей F и G.

Выход: истина, если ; ложь в противном случае.

DERIVES (F,G)

Дата добавления: 2014-01-11