Построение доверительных интервалов

Интервальное оценивание неизвестных параметров.

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. Поэтому в таком случае лучше пользоваться интервальными оценками, то есть указывать интервал, в который с заданной вероятностью попадает истинное значение оцениваемого параметра. Разумеется, чем меньше длина этого интервала, тем точнее оценка параметра. Поэтому, если для оценки Θ* некоторого параметра Θ справедливо неравенство | Θ* - Θ | < δ, число δ > 0 характеризует точность оценки (чем меньше δ, тем точнее оценка). Но статистические методы позволяют говорить только о том, что это неравенство выполняется с некоторой вероятностью.

Определение 1. Надежностью (доверительной вероятностью) оценки Θ* параметра Θ называется вероятность γ того, что выполняется неравенство | Θ* - Θ | < δ. Если заменить это неравенство двойным неравенством – δ < Θ* - Θ < δ, то получим:

p (Θ* - δ < Θ < Θ* + δ) = γ.

Таким образом, γ есть вероятность того, что Θ попадает в интервал (Θ* - δ, Θ* + δ).

Определение 2. Доверительным называется интервал, в который попадает неизвестный параметр с заданной надежностью γ.

1. Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии.

Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим σ, и требуется по значению выборочного среднего 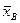оценить ее математическое ожидание а. Будем рассматривать выборочное среднее 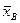как случайную величину 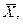а значения вариант выборки х ₁, х ₂,…, х_п как одинаково распределенные независимые случайные величины Х ₁, Х ₂,…, Х_п, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М (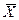) = а, 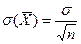(используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства 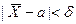. Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:

р (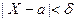) = 2Ф.

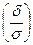Тогда, с учетом того, что

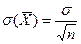, р (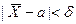) = 2Ф=

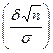=2Ф(t), где .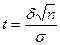

Отсюда 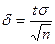, и предыдущее равенство можно переписать так:

. (1)

Итак, значение математического ожидания а с вероятностью (надежностью) γ попадает в интервал , где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.

Пример. Найдем доверительный интервал для математического ожидания нормально распределенной случайной величины, если объем выборки п = 49, 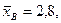σ = 1,4, а доверительная вероятность γ = 0,9.

Определим t, при котором Ф(t) = 0,9:2 = 0,45: t = 1,645. Тогда

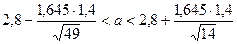, или 2,471 < a < 3,129. Найден доверительный интервал, в который попадает а с надежностью 0,9.

2. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии.

Если известно, что исследуемая случайная величина Х распределена по нормальному закону с неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее математического ожидания построим новую случайную величину

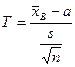, (2)

где 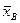- выборочное среднее, s – исправленная дисперсия, п – объем выборки. Эта случайная величина, возможные значения которой будем обозначать t, имеет распределение Стьюдента с k = n – 1 степенями свободы.

Поскольку плотность распределения Стьюдента

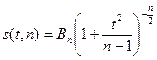, где ,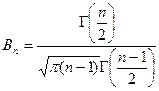

явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- t_γ, t_γ), учитывая четность плотности распределения, следующим образом: .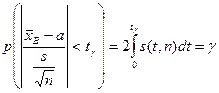

Отсюда получаем:

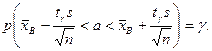(3)

Таким образом, получен доверительный интервал для а, где t_γ можно найти по соответствующей таблице при заданных п и γ.

Пример. Пусть объем выборки п = 25, 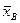= 3, s = 1,5. Найдем доверительный интервал для а при γ = 0,99. Из таблицы находим, что t_γ (п = 25, γ = 0,99) = 2,797.

Тогда 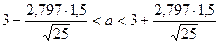, или 2,161< a < 3,839 – доверительный интервал, в который попадает а с вероятностью 0,99.

3. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения.

Будем искать для среднего квадратического отклонения нормально распределенной случайной величины доверительный интервал вида (s – δ, s +δ), где s – исправленное выборочное среднее квадратическое отклонение, а для δ выполняется условие: p (|σ – s | < δ) = γ.

Запишем это неравенство в виде: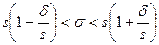или, обозначив ,

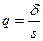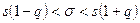. (4)

Рассмотрим случайную величину χ, определяемую по формуле

,

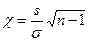которая распределена по закону «хи-квадрат» с п -1 степенями свободы. Плотность ее распределения

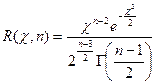
не зависит от оцениваемого параметра σ, а зависит только от объема выборки п. Преобразуем неравенство (4) так, чтобы оно приняло вид χ₁ < χ < χ₂. Вероятность выполнения этого неравенства равна доверительной вероятности γ, следовательно, 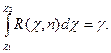Предположим, что q < 1, тогда неравенство (4) можно записать так:

,

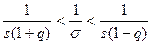или, после умножения на 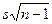, 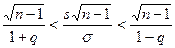. Следовательно,

.

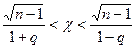Тогда 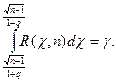Существуют таблицы для распределения «хи-квадрат», из которых можно найти q по заданным п и γ, не решая этого уравнения. Таким образом, вычислив по выборке значение s и определив по таблице значение q, можно найти доверительный интервал (4), в который значение σ попадает с заданной вероятностью γ.

Замечание. Если q > 1, то с учетом условия σ > 0 доверительный интервал для σ будет иметь границы

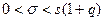. (5)

Пример. Пусть п = 20, s = 1,3. Найдем доверительный интервал для σ при заданной надежности γ = 0,95. Из соответствующей таблицы находим q (n = 20, γ = 0,95) = 0,37. Следовательно, границы доверительного интервала: 1,3(1-0,37) = 0,819 и 1,3(1+0,37) = 1,781. Итак, 0,819 < σ < 1,781 с вероятностью 0,95.

Дата добавления: 2014-01-11