Следствия из аксиом линейного пространства

ОПРЕДЕЛЕНИЕ ЛИНЕЙНОГО ПРОСТРАНСТВА

Примеры

ПОЛЕ

Пусть в множестве K корректным образом определены две внутренние операции, т.е.

1) " a, b ÎK $ c = a ⊕ b ÎK; 2) " a, b ÎK $ d = a ⊗ b ÎK;

и эти операции удовлетворяют следующим свойствам:

а¹) a ⊕ b = b ⊕ a – коммутативность; а²) a ⊗ b = b ⊗ a;

б¹) (a ⊕ b)⊕ с = a ⊕(b ⊕ с) – ассоциативность; б²) (a ⊗ b)⊗ с = a ⊗ (b ⊗ с);

в¹) $qÎK а ⊕ q = а – нейтральный; в²) $ е ÎK а ⊗ е = а;

г¹) " а ÎK $ b ÎK (a ⊕ b)=q – противоположный;

г²) " а ÎK (a ¹q) $ b ÎK a ⊗ b = е, и, кроме того,

д) (a ⊕ b)⊗ с = a ⊗ c ⊕ b ⊗ с – операция ⊗ дистрибутивна по операции ⊕.

Множество K, с так введенными операциями, называется полем.

Отметим, что поле по операции 1) является абелевой группой (свойства а¹, б¹, в¹, г¹). Кроме того, поле по операции 2) после исключения из множества элемента нейтрального по операции 1), является абелевой группой (свойства а²,б², в², г²) и, кроме того, операции 1) и 2) связаны законом дистрибутивности операции 2) по операции 1). (Так называемый 1-й дистрибутивный закон). Отметим, что операция 1), вообще говоря, не дистрибутивна по операции 2).

Q – поле рациональных чисел.

R – поле вещественных чисел.

C – поле комплексных чисел.

Def. Множество V называется линейным (векторным) пространством над числовым полем K, если на множестве V корректным образом заданы две операции: одна - внутренняя, в дальнейшем именуемая сложением и обозначаемая ⊕, другая – внешняя над полем K, в дальнейшем именуемая умножением на скаляр и обозначенная ⊙, удовлетворяющие аксиомам:

I. " x, y Î V $ z Î V | z = x ⊕ y:

1) x ⊕ y = y ⊕ x; 2) (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z);

3) $qÎ V x ⊕ q = q ⊕ x = x; 4) " x Î V $ y Î V x ⊕ y = q.

Эти аксиомы определяют абелеву группу по сложению.

II. " x Î V "aÎK $ z Î V | z = a ⊙ x:

1) 1ÎK 1 ⊙ x = x; 2) " x Î V "a, bÎK a ⊙ (b ⊙ x) = (a ⊙ b) ⊙ x.

III. Эти операции связаны соотношениями:

1) "a, bÎK " x Î V (a + b) ⊙ x = a ⊙ x ⊕ b ⊙ x;

2) "aÎK " x, y Î V a ⊙ (x ⊙ y) = a ⊙ x ⊕ a ⊙ y.

Линейное пространство, заданное над полем вещественных чисел, называется вещественным линейным пространством, а над полем комплексных чисел называется комплексным линейным пространством.

Элементы линейного (векторного) пространства называются векторами.

1°. Нулевой (нейтральный) элемент пространства единственен.

◀ Пусть имеется два нулевых элемента q₁ и q₂. Тогда

1. x ⊕ q₁ = x (Положим в этом равенстве x = q₂). Получим q₂ ⊕ q₁ = q_2.

2. x ⊕ q₂ = x (Аналогично положим x = q₁). Получим q₁ ⊕ q₂ = q₁. У равенств полученных в первой и во второй строках левые части равны, следовательно, правые части также равны Þ q₂ = q₁. ▶

2°. Противоположный вектор к вектору x единственен.

◀ Пусть y и z - элементы противоположные x. Тогда

y = y ⊕ q = y ⊕ (x ⊕ z) = (y ⊕ x) ⊕ z = q ⊕ z = z; Þ y = z. ▶

3°. 0⊙ x = q.

◀ 0⊙ x ⊕ y = 0⊙ x ⊕ y ⊕ q = 0⊙ x ⊕ y ⊕ x ⊕(– x) = (0 + 1)⊙ x ⊕(– x) ⊕ y =

= x ⊕ (– x) ⊕ y = q ⊕ y = y, т.е. 0⊙ x ⊕ y = y Þ 0⊙ x = q. ▶

4°. " x (–1)⊙ x – его противоположный элемент.

◀ x ⊕ (–1)⊙ x = 1⊙ x ⊕ (–1)⊙ x = (1 – 1)⊙ x = 0⊙ x = q. ▶

5°. a⊙q = q.

◀ a⊙q = a⊙(q ⊕ q) = a⊙q ⊕ a⊙q. Прибавим к левой и правой части элемент противоположный a⊙q, т.е. (– a⊙q). Получим в левой части a⊙q ⊕(– a⊙q) = q, а в правой части a⊙q ⊕ a⊙q ⊕(– a⊙q) = a⊙q ⊕ q = a⊙q. Следовательно a⊙q = q. ▶

6°. Если a ⊙ х = q, то a = 0 или x = q.

◀ Если a = 0, то равенство выполнено (см. 3°). Если a ¹ 0, то

x = 1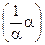⊙ x= ⊙ x = 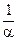⊙(a⊙ x) = 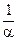⊙q = q, т.е. x = q. ▶

Замечание: В дальнейшем, если это не будет приводить к недоразумениям, будем пользоваться знаком + вместо ⊕, а знак ⊙ будем опускать.

Дата добавления: 2014-01-11