Канонический вид квадратичных форм

Учитывая, что элементы матрицы квадратичной формы a_ij = j(e_i, e_j) мы можем заклю­чить, что элементы матрица квадратичной формы зависят от выбора базиса.

Если для формы j(х, х) в пространстве V существует базис в котором матрица j(х, х) имеет диагональный вид (т.е. a_ij = 0 для i ¹ j), и следовательно форма j(х, х) записы­вается так то такой базис называется каноническим базисом j(х, х) в пространстве V а запись формы в этом базисе называется каноническим видом формы.

Постановказадачи: Для формы j(х, х) ¹ 0 найти базис, в котором форма имеет канони­ческий вид.

Метод Лагранжа (метод выделения полных квадратов) приведения формы к канони­ческому виду.

Пусть в некотором базисе форма имеет вид: .

1). Пусть a_ii = 0 (" i), но $ a_ij ¹ 0. Не ограничивая общности можно считать, что а ₁₂ ≠ 0. Тогда и получим 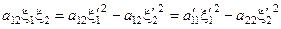(в записи формы появились члены, содержащие квадраты координат).

2). $ a_ii ¹ 0. Допустим, что а ₁₂ ≠ 0. Тогда:

.

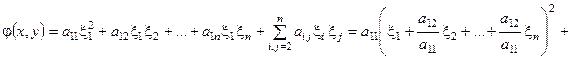
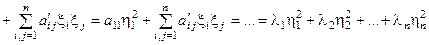При этом: .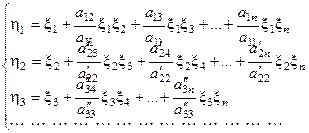

Связь между координатами ξ _i и η _i позволяет установить векторы нового базиса .

Пример:

=

= == .

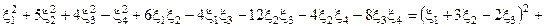
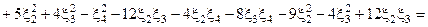
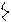
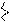
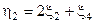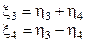
При этом , т.е. .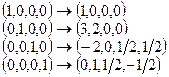

Векторы нового базиса е ₁, е ₂, е ₃, е ₃, получаются из старых f ₁, f ₂, f ₃, f ₄ так:

e ₁ = f ₁; e ₂ = 3 f ₁ + 2 f ₂; e₃ = –2 f ₁ + 0,5 f ₃ + 0,5 f ₄; e₄ = 0,5 f ₃ – 0,5 f ₄.

Метод Якоби приведения формы к каноническому виду.

Пусть форма j(x, x) в базисе имеет матрицу А, где a_ik = j(f_i, f_k); и, при этом, главные миноры матрицы квадратичной формы отличны от нуля: D₁¹0, D₂¹0, D₃¹0, …, D _n = det A ¹0. Форма j(x, x) в базисе имеет вид: j(x, x) =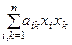. Требуется найти базис { e ₁, e ₂, …, e_n }, чтобы j(e_i, e_k) = 0 (i ¹ k). Векторы канонического базиса { e ₁, e ₂, …, e_n }, ищем из соотно­шений:

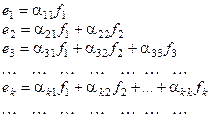. (1)

При этом, нетрудно заметить, что ℒ(е ₁, е ₂, …, е_n) = ℒ(f ₁, f ₂,…, f_n). Отметим, что если j(e_k, f_i) = 0, i = 1, 2, …, k –1, то j(e_i, e_k) = 0 i = 1, 2, …, k –1. В счамом деле

j(e_i, e_k) = j(e_k, a _{i 1} f ₁ + a _{i 2} f ₂ + … + a _iif_i) = 0.

Тогда коэффициенты a _ij будем искать из соотношений:

j(e_k, f_i) = 0 (j < k)

j(e_k, f_k) = 1. (*)

Тогда для коэффициентов разложения: e_k = a _{k 1} f ₁ + a _{k 2} f ₂ + a _{k 3} f ₃ +…+ a _knf_n из условий (*),

получим систему уравнений:

j (e_k, f ₁) = a _{k 1}j (f ₁, f ₁) + a _{k 2} j (f ₂, f ₁) + a _{k 3} j (f ₃, f ₁) + … … … + a _kk j (f_k, f ₁) = 0

j (e_k, f ₂) = a _{k 1}j (f ₁, f ₂) + a _{k 2} j (f ₂, f ₂) + a _{k 3} j (f ₃, f ₂) + … … … + a _kk j (f_k, f ₂) = 0

… … … … … … … … … … … … … … … … … … … … … … … …

j (e_k, f_{k- 1}) = a _{k 1}j (f ₁, f_{k- 1}) + a _{k 2} j (f ₂, f_{k -1}) + a _{k 3} j (f ₃, f_{k -1}) + … … + a _kk j (f_k, f_{k -1}) = 0

j (e_k, f_k) = a _{k 1}j (f ₁, f_k) + a _{k 2} j (f ₂, f_k) + a _{k 3} j (f ₃, f_k) + … … … … + a _kk j (f_k, f_k) = 1

Полученная система линейных уравнений имеет единственное решение, ибо ее определи­тель Δ _k ¹ 0. При этом получим, что: j(e_k, e_i) = 0 (k < i), и j(e_k, e_k) ¹ 0.

Запишем:

j (e_k, e_k) = a _{k 1}j (e_k, f ₁) + a _{k 2} j (e_k, f ₂) + a _{k 3} j (e_k, f ₃) + … + a _{kk- 1} j (e_k, f_{k -1}) + a _kk j (e_k, f_k) = a _kk.

Найти a _kk можем из системы уравнений, которая записана выше, по правилу Крамера:

a _kk =. Таким образом, форма j(x, x) в базисе имеет канонический вид:

j(x, x) =, где a₁₁=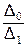, a₂₂=, a₃₃=, …, a _nn =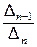. Здесь D₀ = 1.

Пример приведения квадратичной формы к каноническому виду методом Якоби.

Пусть форма: 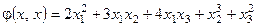задана в базисе f ₁(2, 0, 0), f ₂(0, 1, 0), f ₃(0, 0, 1), а полярная ей билинейная форма имеет вид:

.

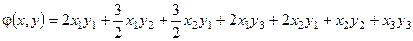Матрица билинейной формы и соответствующей ей квадратичной формы равна: 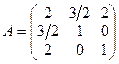и ее главные миноры: D₁ = 2; D₂ = –1/4; D₃ = –17/4. Векторы е ₁, е ₂, е ₃ ищем в виде:

e ₁ = a₁₁ f ₁ = (a₁₁,0,0), e ₂ = a₂₁ f ₁ + a₂₂ f ₂ = (a₂₁, a₂₂, 0), e ₃ = a₃₁ f ₁ + a₃₂ f ₂ + a₃₃ f = (a₃₁, a₃₂, a₃₃).

Получаем:

а) j(e ₁, f ₁) = 1 Þ 2a₁₁ = 1 ® a₁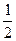₁ = Þ e ₁;

б) 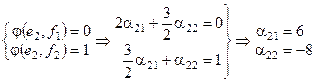Þ е ₂(6, –8, 0);

в) ÞÞ

.

Получены векторы канонического базиса:

e ₁= 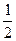f ₁; е ₂(6, –8, 0) = 6 f ₁ – 8 f ₂; = 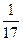(8 f ₁ –12 f ₂ + f ₃)

и в этом базисе форма j(х, х) имеет канонический вид:

.

Дата добавления: 2014-01-11