Двойной интеграл. Основные понятия. Геометрический смысл

КРАТНЫЕ ИНТЕГРАЛЫ

ТЕМАТИЧЕСКИЙ ПЛАН

Тема 1. Кратные интегралы.

Задача, приводящая к понятию двойного интеграла. Вычисление двойного интеграла в прямоугольной и полярной системах координат. Геометрические и физические приложения двойного интеграла. Тройной интеграл. Способы вычисления тройного интеграла. Приложение тройного интеграла.

Тема 2. Криволинейные интегралы.

Понятие криволинейного интеграла II рода. Способы вычисления криволинейного интеграла. Формула Остроградского-Грина. Приложения криволинейных интегралов.

Тема 3. Элементы теории поля.

Скалярное поле. Производная по направлению. Градиент. Векторное поле. Поток, дивергенция, циркуляция, ротор векторного поля. Специальные виды векторных полей.

Тема 4. Числовые и степенные ряды.

Основные понятия числовых рядов. Признаки сходимости числовых рядов. Знакочередующиеся ряды. Абсолютная и условная сходимость знакопеременных рядов. Степенные ряды. Интервал сходимости степенного ряда. Ряды Тейлора и Маклорена. Приложения степенных рядов.

Тема 5. Ряды Фурье.

Периодические функции и периодические процессы. Ряд Фурье. Разложение в ряд Фурье четных и нечетных функций. Представление непериодической функции рядом Фурье.

Тема 6. Элементы операционного исчисления.

Определение функции оригинала и функции изображения. Свойства преобразований Лапласа. Таблица оригиналов и изображений. Операционный метод решения линейных дифференциальных уравнений и их систем.

Пусть в области D плоскости Oxy задана непрерывная положительная функция z = f(x, y).

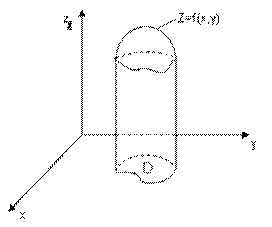Определение: Часть пространства, ограниченную снизу плоскостью Oxy, сверху поверхностью z = f(x,y) и с боков цилиндрической поверхностью, образующая которой параллельна оси Oz, направляющей служит контур области D, называется цилиндрическим телом. Плоскую область D называют основанием этого цилиндрического тела.

Рис. 1

Рассмотрим геометрическую задачу: вычислить объём V цилиндрического тела, ограниченного снизу основанием D, а сверху поверхностью z = f(x,y), где f(x,y) > 0 (рис.1).

Рис. 2

Решение: Известно, что объём цилиндра, ограниченного параллельными плоскостями, равен площади основания цилиндра умноженного на его высоту. В общем случае, когда цилиндр ограничен сверху произвольной поверхностью z=f(x,y), поступим следующим образом. Разобьём область D (проекция поверхности z=f(x,y ) на плоскость Оxy) произвольным образом на n частей (областей) D_i, площади которых равны (рис.2). Рассмотрим цилиндрические столбики с основанием D_i, ограниченные сверху кусками поверхности z=f(x,y). В своей совокупности они составляют тело V. , - объем столбика с основанием D_i,.

Возьмём на каждой площадке произвольную точку M_i(x_i,y_i) и заменим каждый столбик прямым цилиндром с тем же основанием D_i, и высотой z _i=f(x_i,y_i) (рис. 3). Найдем объем каждого цилиндрического столбика: .

Т.о. построим цилиндрическое ступенчатое тело, объём которого можно считать приближенным значением искомого объема. 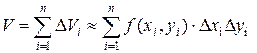. Это равенство тем точнее, чем больше число n и чем меньше размеры области D_i,.

Рис. 3

Начнем неограниченно увеличивать число площадок . Диаметр (наибольшее расстояния между точками принадлежащими области D) будет стремиться к нулю , то есть каждая площадка будет стягиваться в точку. При этом ступенчатое тело будет всё плотнее заполнять данное цилиндрическое тело, а объём V_n будет изменяться, стремясь к некоторому пределу. Естественно принять за величину объема V данного цилиндрического тела тот предел, к которому стремится V_n при , то есть .

Отвлекаясь от геометрического смысла полученного предела, его называют двойным интегралом от функции z=f(x,y) по области D и обозначают .

Итак, двойной интеграл определяется равенством

.

Величина двойного интеграла от неотрицательной функции равна объёму цилиндрического тела - геометрический смысл двойного интеграла.

Функцию z =f(x,y) называют подынтегральной функцией, D- область интегрирования, dxdy (или ds) - элемент площади.

Существует теорема, согласно которой для любой функции f(x,y) непрерывной в области D, существует двойной интеграл, величина которого не зависит ни от способа разбиения области D на части, ни от выбора точки M_i(x_i,y_i) в каждой из частей.

Сравнивая определения двойного интеграла для функции двух переменных с определением определённого интеграла для функций одной переменной, нетрудно убедится в полной их аналогичности. Аналогичны и свойства этих интегралов.

Дата добавления: 2014-01-11