Вычисление двойного интеграла в декартовых координатах

Свойства двойного интеграла

1) константу можно выносить за знак интеграла

2) интеграл от алгебраической суммы двух функций равен сумме двух интегралов

3) если область D разбить линией на две области D₁ и D₂ такие, что D₁UD₂=D, то

4) 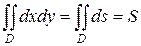т.к.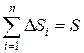

Требуется вычислить двойной интеграл , где функция z=f(x,y)≥0 непрерывна в области D. Как мы выяснили двойной интеграл выражает объём цилиндрического тела, ограниченного сверху поверхностью z=f(x,y).

Согласно методу параллельных сечений 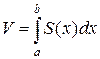, где S(x) -площадь сечения плоскостью, перпендикулярной оси Ох, х=а, х=b - уравнение плоскостей, ограничивающих данное тело.

Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми х=а, х=b и кривыми , (рис. 4). Функции и непрерывны и для всех .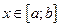

Определение. Область D называется правильной в направлении оси Oy, если любая прямая параллельная оси Oy, пересекает границу области не более, чем в двух точках.

Точка - точка входа,

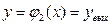- точка выхода.

Рис. 4

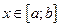Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох: х=const, . В сечении получим криволинейную трапецию ABCD, ограниченную линиями 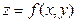, где х=const, z=0, , (рис. 5).

Площадь S(x) этой трапеции находим с помощью определённого интеграла

Далее, так как это равенство записывают в виде (1.2.1)

	Рис. 5

Т.о. согласно формуле (1.2.1) вычисления двойного интеграла сводятся к последовательному вычислению двух определённых интегралов.

Правую часть формулы (1.2.1) называют двукратным интегралом от функции f(x,y) по области D. При этом называется внутренним интегралом.

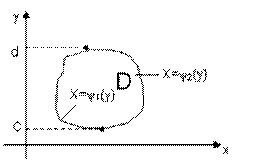Для вычисления двукратного интеграла сначала берём внутренний интеграл, считая x - постоянным, затем берём внешний интеграл, т.е. результат первого интегрирования интегрируем по x в пределах от а до b.

Если область D ограничена прямыми y=c, y=d (c<d), кривыми ,причём 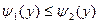для 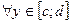, т.е. область D - правильная в направлении оси Ox (рис. 6). То, рассекая тело плоскостью y=const, аналогично получим

Рис. 6

(1.2.2)

Здесь при вычислении внутреннего интеграла считаем y-const

Замечания.

1) Формулы (1.2.1) и (1.2.2) справедливы в случае, когда f(x,y)<0 .

2) Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле 1.2.1, так и по формуле 1.2.2.

3) Если область D не является правильной ни по x ни по y, то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ox или оси Oy.

4) Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.

Пример:

Вычислить двойной интеграл , , .

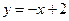Решение:

Строим область интегрирования (рис. 7). В данном примере удобнее вычислять интеграл по формуле (1.2.2), в направлении оси Ох.

Рис. 7

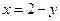
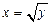
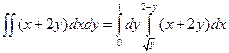
Вычисляем внутренний интеграл, y-const

.

Полученную функцию интегрируем по х

Можно было воспользоваться формулой (1.2.1), но для этого область D следует разбить на две области D₁ и D₂ (рис. 8).

Рис. 8

Вычислить самостоятельно двойные интегралы в правой части. Получить тот же результат 29/20.

Дата добавления: 2014-01-11