Формула Тейлора

Ряды Тейлора и Маклорена

Наиболее простой функцией среди элементарных является многочлен. Он легко дифференцируется и интегрируется. Значения многочлена вычисляются так же значительно легче, чем других функций. В связи с этим встает вопрос, нельзя ли другие, более сложные функции заменить многочленами, не допуская при этом больших погрешностей. Этот вопрос положительно решен по отношению к некоторым функциям с помощью, так называемой формулы Тейлора.

Предположим, что функция f(x) имеет все производные до (n+1) -го порядка включительно, в некотором промежутке, содержащем точку х=а.

Найдем многочлен 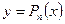степени не выше n, значение которого в точке х=а равняется значению функции f(x) в этой точке, а значения его производных до n -го порядка в точке х=а равняются значениям соответствующих производных от функции f(x) в этой точке, т.е. удовлетворяют условиям:

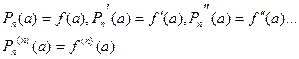(4.5.1)

Будем искать этот многочлен в виде

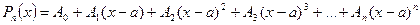(4.5.2)

Задача – определить коэффициенты .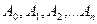

Продифференцируем многочлен 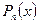n раз

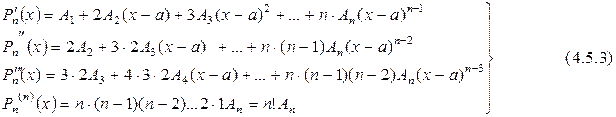
Подставим в формулу (4.5.2) и формулы (4.5.3) значение х=а, получим, используя условие (4.5.1)

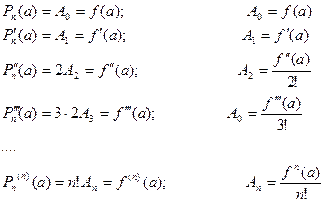
Получим искомый полином

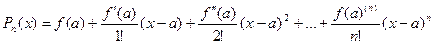
Обозначим разность значений данной функции 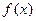и построенного многочлена 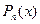, т.е. .

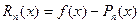Получаем 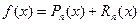или

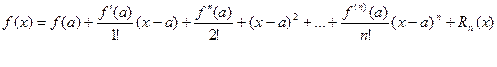
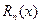- ошибка, которую допускаем, заменяя данную функцию 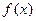многочленом. 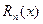называется остаточным членом. Для тех значений х, при которых величина 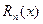мала по сравнению с величиной 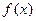, многочлен дает удовлетворительное “сближение” значени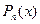й и 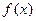. Т.о., имеется возможность заменить функцию y=f(x) многочленом 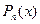с соответствующей степенью точности, равной значению остаточного члена .

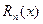В полном курсе математического анализа доказывается, что остаточный член можно записать в форме Лагранжа:

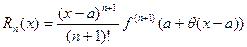
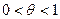
В итоге получаем формулу Тейлора для функции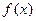

   

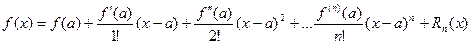
Если в формуле Тейлора положить a=0, то получаем частный случай формулы Тейлора – формулу Маклорена:

 

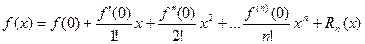
Обе формулы представляют собой степенные ряды, которые называются рядом Тейлора и рядом Маклорена.

Ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции в окрестности точки а, но отсюда ещё не следует, что он будет сходиться к данной функции. Ряд может оказаться расходящимся или сходящимся, но не к функции .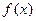

Теорема 1. Для того чтобы ряд Тейлора, функции 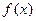, сходился к самой функции в точке х, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора стремился к нулю при 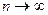, т.е. чтобы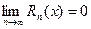

На практике пользуются ещё одной теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора.

Теорема 2. Если модули всех производных функции 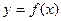ограничены в окрестности точки х=а одним и тем же числом 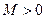, то для любого х из этой окрестности ряд Тейлора функции 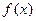сходится к функции 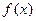, т.е. имеет место разложение

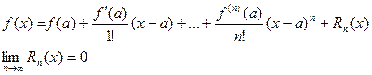
Дата добавления: 2014-01-11