Оригиналы и их изображение

ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

Операционное исчисление играет важную роль при решении прикладных задач, особенно в современной автоматике и телемеханике.

Основными первоначальными понятиями операционного исчисления являются понятия функции – оригинала и функции-изображения.

Пусть f(t) – действительная функция действительного переменного t (под t понимается время или координата)

Определение. Функция f(t) называется оригиналом, если она удовлетворяет следующим условиям:

1) f (t) = 0 при t < 0

2) f (t) – кусочно-непрерывная при t 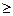0

3) существуют такие числа M > 0 и S₀ 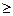0, что для всех t выполняется неравенство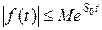, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции.

Число S₀ называется показателем роста f(t).

Функция f(t) называется кусочно-непрерывной, если она непрерывна или имеет точки разрываI рода, причем на каждом конечном промежутке оси t лишь конечное число.

Условия (1-3) выполняются для большинства функций, описывающих различные физические процессы. Первое условие означает, что процесс начинается с некоторого времени; удобнее считать, что в момент t=0. Третьему условию удовлетворяют ограниченные функции (для них S₀=0), степенные 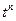(n > 0) и другие. Для функций вида 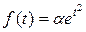, условие 3 не выполняется; не является оригиналом и функция f(t)=- не выполняется 2-е условие.

Определение. Изображением оригинала f(t) называется функция F(p) комплексного переменного р=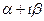, определяемая интегралом

.

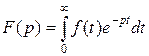Операцию перехода от оригинала f(t) к изображению F(p) называют преобразованием Лапласа. Соответствие между оригиналом f(t) и изображением F(p) записывается в виде f(t) ÷ F(p). Принято оригиналы обозначать малыми буквами, а их изображения – соответствующими большими.

Пример 1.

Простейшим оригиналом является функция Хевисайда, определяемая следующим образом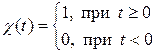

Найдем изображение этой функции

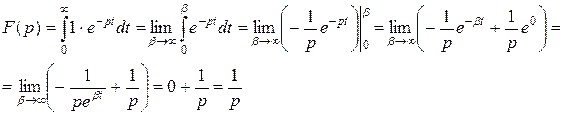
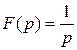, в символической записи .

Замечание: В дальнейшем функцию – оригинал будем коротко записывать в виде f(t), подразумевая, что.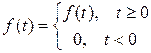

Пример 2. Найти изображение функции 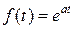, а – любое число.

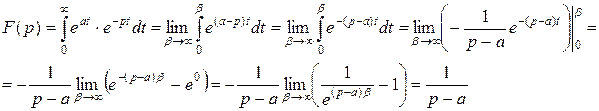
Получили .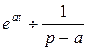

Пример 3. f(t) = t. Найти изображение. Пользуясь определением изображения составляем интеграл

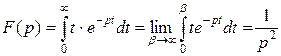(вычислить интеграл самостоятельно, применив формулу интегрирования по частям).

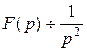
Дата добавления: 2014-01-11