Методы комплексной области

Задание оператора преобразования уравнениями состояния

Рассмотрим одномерное, непрерывное, стационарное ЛДЗ с оператором преобразования A_t, который задан неявно линейными уравнениями состояния

где A, B, C –матрицы соответствующих размеров; d – скалярная матрица (число).

Общее решение этого уравнения имеет следующий вид:

.

Здесь у ₁(t) 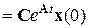- составляющая процесса, обусловленная ненулевыми начальными условиями; 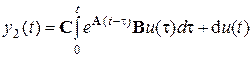- частное решение, соответствующее нулевым начальным условиям. При известном входном сигнале, y ₂(t) можно представить как сумму вынужденной и «собственной сопровождающей» выхода: y ₂(t)= y ₂₁(t)+ y ₂₂(t). При этом вынужденная составляющая y ₂₁(t) имеет вид (форму) вынуждающей функции – входа u (t).

Для устойчивого ЛДЗ составляющие выхода у ₁(t) и y ₂₂(t) затухают во времени и на выходе остается только вынужденная составляющая y ₂₁(t). При этом условием затухания является «левое» расположение собственных значений матрицы A, т.е. корней характеристического уравнения det(p E - A)=0. Если порядок матрицы А не слишком большой, то раскрыв определитель полиномиальной матрицы, можно найти коэффициенты характеристического полинома и исследовать устойчивость рассмотренными выше алгебраическими критериями (например критерием Гурвица). Но при большой размерности матрицы А (сотни и выше)получение этих коэффициентов с достаточной точностью проблематично. В таких случаях применяется матричный критерий Зубова, суть которого состоит в следующем.

С помощью подстановки 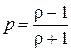характеристическое уравнение преобразуется к виду det(p E - A _x)=0, где A _x=(E + A)(E - A)^-1. Критерий Зубова формулируется относительно матрицы A _x в разных формах:

1) необходимая и достаточная: (A _x) ^k ® 0 при k ®¥;

2) необходимая форма: Sp A _x < n, если система устойчива;

3) достаточная форма I: ||(A _x) ^k || <1 при некотором k;

4) достаточная форма II: Sp A _x ^k > Sp A _x ^{k +1}> Sp A _x ^{k +2} при некотором k.

Здесь Sp A _x = - след матрицы (сумма диагональных элементов);

||(A _x)|| - любая из норм матрицы, например «евклидова» норма - квадратный корень из суммы квадратов всех элементов матрицы.

Критерий Зубова и его разновидности ориентированы на компьютерные вычисления при исследовании устойчивости сложных ЛДС, имеющих высокий порядок. Если при больших значениях степени матрицы A _x критерий не дает ответа, то считают, что ЛДС либо не устойчива, либо имеет малые запасы устойчивости, что с практической точки зрения одно и то же.

Методы временной области, в принципе, позволяют провести исследование свойств и динамических особенностей ЛДС и их составляющих (звеньев). Однако они сложны для практического применения даже в простых случаях, требуют от проектировщика довольно глубоких математических знаний и, в конечном счете, ориентированы на компьютерные вычисления. Особенно это относится к решению задач синтеза, связанных с выбором структуры и параметров корректирующих устройств, способов их подключения и др.

Бóльшие удобства в этом плане дают методы комплексной области, где вместо функций времени f (t) рассматриваются их операционные изображения в виде функций комплексной переменной F (p). Математические описания (модели) ЛДС в терминах изображений существенно упрощаются, легко решаются и исследуются, а результаты затем, при необходимости, интерпретируются во временной области. Математической основой этой группы методов для непрерывных ЛДС является интегральное преобразование Лапласа.

Дата добавления: 2014-01-11