Основные свойства преобразования Лапласа

1) Линейность: ;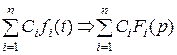

2) Изображение производных: 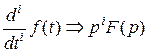- (при нулевых начальных значениях для функции и производных: f (0)= f ⁽¹⁾(0)=…= f ^{( i –1)}(0)=0);

3) Изображение интегралов: ;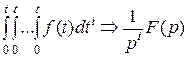

4) Изображение свертки двух функций времени: f ₁(t)Ä f ₂(t)Þ F ₁(p) F ₂(p);

5) Если при t ®¥ f (t) ®0, то все полюса F (p) лежат в левой полуплоскости;

6) Если f (t) не имеет разрывов второго рода (бесконечных скачков, описываемых d-функциями и их производными), то порядок числителя F (p) меньше порядка его знаменателя (m < n).

7) Начальное и конечное (если существует!) значения функции оригинала:

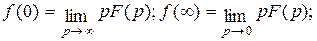
8) Смещение во временной области: f (t –t) Þ F (p) e ^{– p t};

9) Смещение в комплексной области: f (t) e ^{– at} Þ F (p +a);

10) Определение оригинала f (t) по изображению F (p):

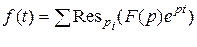, где p_i – полюса выражения F (p).

Напомним, что вычет в некратном полюсе p_i вычисляется по формуле

.

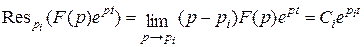Применим эти свойства для изучения ЛДЗ и ЛДС.

А) Пусть для ЛДЗ известна весовая функция w (t), звено находится в покое и на его при t =0 подается сигнал u (t). Тогда y (t)= w (t)Äu(t) и по свойству 4 получим, что y (p)= W (p) u (p), где W (p)= £ { w (t)}. Этот множитель выполняет функцию коэффициента передачи ЛДЗ в комплексной области, который связывает изображения входа и выхода. Его принято называть передаточной функцией ЛДЗ. В соответствии с этим, можно дать другое, но эквивалентное определение для W (p) как отношение изображений Лапласа выхода y (p) и входа u (p) при нулевых начальных условиях. Отметим, что (свойство 5) для устойчивого ЛДЗ все полюса W (p) должны быть «левыми», т.к. только в этом случае w (t) будет затухать до нуля.

Б) Пусть оператор преобразования ЛДЗ задан уравнением «вход-выход»:

A (D) y (t)= B (D) u (t),

где A (D) = a ₀+ a ₁ D + a ₂ D ²+…+ a_nDⁿ, B (D) = b ₀+ b ₁ D + b ₂ D ² +…+ b_mD^m, D = d / dt.

Преобразуя по Лапласу (при нулевых начальных условиях!) обе части этого уравнения и используя свойства 1 и 2, получим

A (p) y (p)= B (p) u (p),

где A (p) = a ₀+ a ₁ p + a ₂ p ²+…+ a_npⁿ, B (p) = b ₀+ b ₁ p + b ₂ p ² +…+ b_mp^m. Отсюда следует, что y (p)= A ^-1(p) B (p) u(p)= W (p) u(p), где W (p)= B (p)/ A (p) – передаточная функция ЛДЗ.

Таким образом, передаточную функцию ЛДЗ можно определить и как отношение операторных полиномов правой и левой частей уравнения «вход-выход», если заменить в них символа оператора дифференцирования D на комплексную переменную p. Заметим, что в знаменателе выражения для W (p) в этом случае будет характеристический полином A (p), корни которого p_i определяют свойство устойчивости ЛДЗ. Для устойчивого звена все p_i должны быть «левыми».

Поскольку y (p) = B (p)/ A (p) u(p), то полюса y (p) можно разделить на две группы: p_i – полюса передаточной функции и p_j – полюса изображения входа u(p). Тогда

.

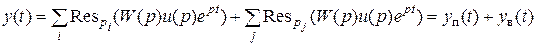Таким образом, реакция линейного динамического звена на некоторое входное воздействие u(t) может быть представлена суммой переходной y _п(t) и вынужденной составляющей y _в(t). Для устойчивого звена y _п(t) асимптотически затухает, а полная реакция y (t) стремится к вынужденной составляющей y _в(t).

Передаточная функция W (p) позволяет сформулировать условие физической осуществимости ЛДЗ и его оператора A_t в более простом, чем ранее виде. Обозначим m = deg B (p) – порядок числителя, а deg B (p) – порядок знаменателя в W (p). Тогда изображение переходной функции h (p) будет иметь порядки числителя и знаменателя, соответственно m и n +1. Для физической осуществимости ЛДЗ (см. свойство 6) требуется, чтобы m < n +1 или более кратко, m £ n.

С передаточной функцией ЛДЗ связаны понятия минимальной и не минимальной фазовости. Для минимально-фазового звена все нули и полюса передаточной функции располагаются слева от мнимой оси. В противном случае ЛДЗ называется неминимально-фазовым. Сюда, в частности, относятся неустойчивые звенья.

В) Пусть оператор преобразования ЛДЗ задан уравнениями состояния:

, при условии x (0)= 0.

Применяя преобразование Лапласа к этим выражениям, получим:

p x (p)= Ax (p)+ B u (p); y (p)= Cx (p)+d u (p).

Исключив x (p), найдем связь u (p) и y (p) в виде формулы

y (p) = { C [ p E – A ]^–1 B +d} u (p) = W (p) u (p),

где W (p) = C [ p E – A ]^–1 B +d – передаточная функция ЛДЗ.

Из последнего выражения следует, что полюса W (p) будут представлены корнями уравнения det(p E – A) =0, т.е. собственными значениями матрицы A. При этом часть полюсов W (p) может совпадать с корнями ее числителя (нулями). В подобных случаях пары «нуль – полюс» (диполи) «компенсируют» друг друга в реакциях звена, находящегося в покое, на любые внешние воздействия. Это относится и к весовой, и к переходной функции ЛДЗ. Но полюса, входящие в диполи, будут влиять на характер свободного движения в ЛДЗ за счет ненулевых начальных условий, а значит и на его устойчивость. Для таких ЛДЗ передаточная функция, а также весовая и переходная функции, характеризуют полностью только управляемую и наблюдаемую часть его ММ.

Дата добавления: 2014-01-11