Частотные критерии устойчивости

Исходные данные для этой группы критериев устойчивости представляют собой либо некоторые частотно-зависимые комплекснозначные функции, либо частотные характеристики разомкнутых систем. Их математической основой является принцип аргумента для функции комплексной переменной в виде полинома (частотное свойство полиномов).

4.1. Частотное свойство полинома. Рассмотрим полином n -го порядка с вещественными коэффициентами и запишем его в факторизованной форме:

. (4.1)

Пусть p = j w, где w - вещественная переменная, изменяющаяся от -¥ до +¥. Подсчитаем при этом изменение аргумента для A (j w):

. (4.2)

Изменение аргумента для элементарного множителя (j w- p_i) зависит от расположения корня p_i относительно мнимой оси:

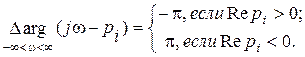(4.3)

Если у A (p) нет мнимых корней, а имеется " r " правых и " n - r " левых корней, то суммарное изменение аргумента для комплекса A (j w) будет равно p(n -2 r).

.

Если переменной w придать физический смысл угловой частоты гармонических колебаний, принимающей только положительные значения, то изменение аргумента Darg A (j w) уменьшится в два раза:

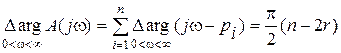. (4.4)

Это «частотное свойство» полинома с вещественными коэффициентами используется для доказательства частотных критериев устойчивости.

4.2. Критерий устойчивости Михайлова (1936 г.). Пусть A (p) – характеристический полином исследуемой ЛДС. При этом структурная схема системы может быть любой. Назовем, для краткости, комплекснозначную функцию A (j w) при изменении w от 0 до ¥ функцией Михайлова M (j w). Из (4.4) следует, что для устойчивой ЛДС, у которой число правых корней r =0, изменение аргумента для M (j w) равно n p/2. Справедливо и обратное утверждение: если Darg M (j w)= n p/2, то r =0 и ЛДС будет устойчивой. Таким образом, для устойчивости ЛДС n -го порядка необходимо и достаточно, чтобы изменение аргумента функции Михайлова было равно n× p/2 (критерий устойчивости Михайлова). Этому критерию можно придать удобную геометрическую интерпретацию: Для устойчивости ЛДС необходимо и достаточно, чтобы годограф функции Михайлова, начинаясь при w=0 на положительной части вещественной оси, последовательно в положительном направлении, нигде не обращаясь в ноль, проходил через n квадрантов комплексной плоскости. В противном случае ЛДС либо неустойчива, либо находится на границе устойчивости.

Если годограф Михайлова при некоторой частоте w₁>0 проходит через начало координат, то среди корней будет два мнимых корня p ₁=+ j w₁ и p ₂=- j w₁. Для выяснения расположения остальных корней необходимо деформировать годограф в малой окрестности начала координат в двух противоположных направлениях. Если при этом для одного деформированного годографа условия критерия выполняются, а для другого не выполняются, то исследуемая ЛДС находится на колебательной границе устойчивости. В случае, когда w₁=0 ЛДС находится на апериодической границе устойчивости (с нулевым корнем).

Для систем, порядок которых не выше четвертого, удобна аналитическая форма критерия Михайлова. При этом для устойчивости ЛДС требуется выполнение следующих условий:

1) Re M (j 0) > 0; 2) 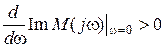; 3) w₀<w₁<w₂<...<w _{n -1},

где w₀, w₂, w₄,... - неотрицательные корни уравнения Im M (j w)=0;

w₁, w₃, w₅,...- неотрицательные корни уравнения Re M (j w)=0.

На этих частотах годограф Михайлова пересекается с координатными осями и при таком их соотношении он соответствует устойчивой ЛДС.

Корни уравнения для вещественной части можно не находить, а ограничиться только проверкой знаков Re M (j w) на частотах w₀, w₂, w₄, и т.д. Если при этом знаки вещественной части чередуются, то ЛДС будет устойчивой.

Сделаем несколько замечаний относительно способов расчета и построения точек годографа Михайлова:

1) Годограф Михайлова всегда начинается при w=0 в точке a ₀ на вещественной оси, а при w®¥ устремляется (если a_n >0) в квадрант с номером n.

2) Так как с возрастанием w модуль | M (j w)| быстро увеличивается, то для удобства графических построений можно рассматривать масштабированную функцию Михайлова M* (j w), получаемую делением M (j w), например, на выражение вида (| a ₀| + | a_n |w ⁿ). В этом случае M* (j w) = jⁿ.

3) При известной матрице A в уравнениях состояния ЛДС, для компьютерных расчетов точек годографа используется формула M (j w)=det (j w E - A).

4) Для ЛДС со сложной структурой, заданной матрицей взаимных связей звеньев R _y и передаточными функциями звеньев W_i (p)= B_i (p)/ A_i (p), целесообразно компьютерный расчет точек годографа выполнять по формуле:

М (j w) = det (A *(j w)- B *(j w) R _y), (4.5)

где A *=diag{ A_i (j w)}, B *(j w)=diag{ B_i (j w)}.

Критерий Михайлова можно применять как для замкнутых и для разомкнутых систем с любой структурой, и в этом смысле он аналогичен алгебраическим критериям. Но аналогичными будут и проблемы оценки запасов устойчивости САР и связи их со значениями параметров системы. Это ограничивает использование критерия Михайлова для решения задач динамического синтеза САР.

Дата добавления: 2014-01-11