Разностные уравнения

Построение кривых переходного процесса

Теоретически кривая переходного процесса получается при решении дифференциального уравнения операторным методом, путем отыскания оригинала выходного сигнала при заданном типовом воздействии. График решения дифференциального уравнения и является кривой переходного процесса.

В курсе рассматриваются следующие методы построения кривой переходного процесса:

- метод трапецеидальных вещественных частотных характеристик (самостоятельно);

- на основе разностных уравнений.

Построение кривой переходного процесса на основе разностных уравнений предполагает дискретизацию непрерывных (аналоговых) уравнений.

Процесс дискретизации можно представить в виде работы следующего элемента (ключа) (рис. 5.9), где D t – шаг дискретизации.

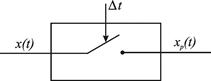
Рис. 5.9. Схема дискретизации переменной

Пусть x (t) – входной сигнал элемента представляет собой решение дифференциального или интегро-дифференциального уравнения (рис. 5.10а). На выходе ключа имеем сигнал x_p(t), представленный на рис. 5.10б, т.е. последовательность импульсов длительностью h, где h – время замыкания ключа. Если h <<D t, то временем замыкания ключа можно пренебречь, что показано на рис. 5.10в.

Математически этот сигнал записывается в виде:

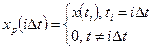. (5.16)

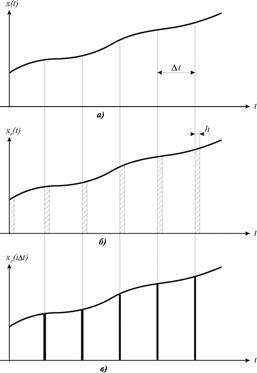
Рис. 5.10. Процесс дискретизации сигнала

и называется такой сигнал дискретным или решетчатым. Время t_i=i D t называется дискретным временем. Если шаг дискретизации постоянный (Dt=const), то вместо дискретного времени t_i=iDt используют аналог дискретного времени i, представляющий собой целое число. Тогда дискретный сигнал записывается в виде x (i), т.е.

x (i)= x_р (iDt). (5.17)

Для получения дискретного сигнала x (i) на основе непрерывного x (t), представляющего собой решение дифференциального или интегро-дифференциального уравнения, достаточно последний дискретизировать с шагом D t в соответствии с выражением (5.17). Например:

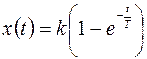, то .

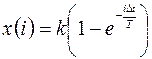Дискретный сигнал x (i) можно получить и путем дискретизации непрерывных (дифференциальных или интегро-дифференциальных) уравнений, т.е. путем перехода к разностным уравнениям. Для получения разностного уравнения достаточно любую дискретную функцию, зависящую от другой дискретной функции представить в рекуррентной форме.

Линейное разностное уравнение n -го порядка записывается в виде:

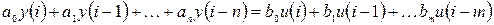, (5.18)

где i – аналог дискретного времени; a₀, a₁,…,a_n, b₀, b₁,…,b_m – коэффициенты разностного уравнения.

Выразив y (i) из уравнения (5.18), получим рекуррентную формулу вида:

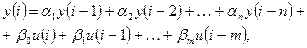(5.19)

где

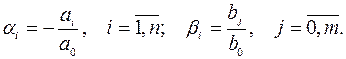
Дата добавления: 2014-01-11