Свойства при статических испытаниях

Прочность при растяжении. Испыта­ние материалов на растяжение — наи­более простое и распространенное. Чтобы результаты испытаний были сравнимы, применяют геометрически подобные образцы, обычно круглого сечения. Образец растягивают на раз­рывной машине с постоянной ско­ростью движения захватов и опреде­ляют зависимость удлинения расчет­ной части образца Δl от нагрузки Р вплоть до разрушения. По этим дан­ным строят диаграмму растяжения (рисунок 3.5), т. е. зависимость относи­тельного удлинения ε = Δl /l₀ от ус­ловного напряжения σ = P/F₀ , где F₀ — площадь поперечного сечения об­разца до деформации.

В начале нагружения между на­пряжением и деформацией существует линейная зависимость, что позволяет при расчетах пользоваться законом Гука. Напряжение, при котором от­ступление от линейной зависимости между напряжением и деформациями впервые достигает некоторой заданной величины, называют пределом про­порциональности σ_пц (точка 1 на рисунке 3.5). Если в какой-либо момент на­чать разгружать образец (точка А), то зависимость между напряжением и деформацией при разгрузке изобра­зится прямой линией АВ, практически параллельной линии нагрузки 01. Де­формация в точке А состоит из упру­гой части ε_упр, которая устраняется после снятия нагрузки, и остаточной (пластической) части ε_ост, которая остается после снятия нагрузки На­пряжение, при котором остаточные деформации впервые достигают не­которой заданной величины (обычно порядка 0,002—0,005%), называют пре­делом упругости σ_у (точка 2) Предел упругости часто считают совпадаю­щим с пределом пропорциональности

При нагружении за пределом упру­гости остаточные деформации заметно увеличиваются Для низкоуглеродистой стали деформация некоторое вре­мя растет без нарастания напряже­ний, что дает площадку текучести (рисунок 3.5) Напряжение, соответствующее площадке текучести, называют пределом текучести σ_Т.

Многие материалы не имеют пло­щадки текучести Для них определяется условный предел текучести — напряжение, при котором остаточные деформации достигают некоторой за­данной величины (обычно 0,2%), ус­ловный предел текучести, соответ­ствующий указанной величине оста­точной деформации, обозначают σ_0.2 (точка 3 на рисунке 3.5)

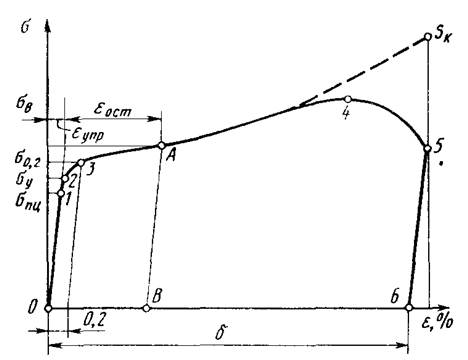
Рисунок 3.5

Вначале образец равномерно растя­гивается по всей длине. При большой деформации происходит потеря устой­чивости пластической деформации и образуется местное сужение — шейка. В результате этого нагрузка, воспри­нимаемая образцом, и условное на­пряжение уменьшаются. А истинное напряжение, определяемое по дей­ствительной минимальной площади поперечного сечения образца, продолжает возрастать, как показано на рисунке 3.5 штриховой линией. Хрупкие материа­лы разрушаются без образования за­метной шейки Максимальное условное напряже­ние, которое выдерживает образец, называют временным сопротивлением, или пределом прочности σ_в (точка 4). Истинное напряжение в момент окон­чательного разрушения образца на­зывают истинным пределом прочно­сти — S_K.

При испытании на растяжение опре­деляют также характеристики пла­стичности материала – относительное удлинение и относительное сужение (уменьшение площади поперечного се­чения) при разрыве.

Относительное удлинение, численно равное отрезку 0—6 (рисунок 3.5), вычисля­ют по формуле

δ= (l_k-l₀)/l₀ *100%,

где l_к — суммарная длина разорвав­шихся участков расчетной части об­разца, l₀ — длина расчетной части образца до деформации

Зависимость между напряжениями и дефор­мациями в реальном материале может быть доста­точно сложной: в зависимости от величины дей­ствующих напряжений деформации могут быть обратимыми (упругими) и необратимыми (пласти­ческими). При напряжениях, не превышающих предела упругости, эта зависимость, как известно, выражается законом Гука, согласно которому де­формации в материале пропорциональны напряже­нию.

В простейшем случае одноосного растяжения элементарного параллелепипеда, например в нап­равлении оси х, в этом направлении он получает от­носительное удлинение, равное:

ε_х=σ_х/Е,

а в направлениях у и z - относительное сужение:

ε_у= νσ_х/Е, ε_z=νσ_х/Е

где Е - модуль упругости материала; ν - коэффициент Пуассона материала.

При напряжениях выше предела текучести в теле возникают пластические деформации, не исчезающие после разгрузки.

В теории пластичности используют две груп­пы математических моделей поведения материа­лов. Их называют теорией упруго-пластических деформаций и теорией течения. В первой группе устанавливают связь между напряжениями и де­формациями. Во второй - между напряжениями и бесконечно малыми приращениями деформаций при бесконечно малых приращениях напряжений. Достоинство моделей первой группы - простота, однако модели этой группы не описывают слож­ного нагружения и не позволяют учитывать исто­рию нагружения при определении пластических деформаций. Модели второй группы свободны от этих ограничений, но более сложны в использовании.

Итак, возможные модели матери:

– упругая;

– упруго-пластическая.

Дата добавления: 2014-01-11