Напівпровідник Діелектрик

Механіки. Воно не може бути доведене з інших співвідношень. Його варто розглядати як вихідне основне припущення, справедливість якого доводиться тим, що всі наслідки, які випливають із нього, точно узгоджуються з дослідними фактами.

Шредінгер установив своє рівняння, виходячи з оптико-механічної аналогії. Ця

аналогія полягає в подібності рівнянь, які описують хід світлових променів, з рівняннями, що визначають траєкторії частинок у класичній механіці.

Пояснимо, як можна прийти до загального рівняння Шредінгера. Для простоти обмежимося одновимірним випадком. Розглянемо частинку, яка вільно рухається.

Відповідно до ідеї де Бройля такій частинці потрібно поставити у відповідність плоску хвилю

Y = A exp[(i / h)(px - Et)].

Продиференцiюємо цю функцію один раз за t, а інший раз – двічі за x й отримаємо

¶ 2 Y

æ i ö 2

Звідси

¶Y= - i E Y,

¶ t h

¶ x 2

= ç ÷ è hø

p Y.

E = 1 i h ¶Y,

p 2= - 1 h2¶

Y. (85.3)

Y ¶ t

Y ¶ x 2

У нерелятивістській класичній механіці енергія E й імпульс p вільної частинки пов'язані співвідношенням

E = p.

2 m

Підставивши в це співвідношення вираз (85.3) для E й отримаємо рівняння

p 2 і скоротивши потім на Y,

2 2

- h ¶ Y = i h ¶y,

2 m ¶ x 2 ¶ t

яке збігається з рівнянням (85.1), якщо в останньому покласти U = 0.

У випадку частинки, що рухається в силовому полі, яке характеризується потенціальною енергією U, енергія E й імпульс p пов'язані співвідношенням

p = E - U.

2 m

Поширивши й на цей випадок вираз (85.3) для E й

p 2, отримаємо

2 2

- 1 h ¶ Y = 1 i h ¶y - U.

Y 2 m

¶ x 2

Y ¶ t

Помножимо це співвідношення на Y й перенесемо доданок U Y

рівняння

ліворуч і прийдемо до

h

2 ¶2

-

Y + U Y = i h ¶y,

яке збігається з рівнянням (85.1).

2 m ¶ x 2 ¶ t

Викладені міркування не мають доказової сили й не можуть розглядатися як

доведення загального рівняння Шредінгера. Їх мета – пояснити, яким чином можна було прийти до встановлення цього рівняння.

2 Якщо силове поле, у якому рухається частинка, є стаціонарним (тобто сталим в

часі), то функція U не залежить явно від t. У цьому випадку розв’язок рівняння Шредінгера розпадається на два множники, один із яких залежить тільки від координат, інший – тільки від часу:

Y(x, y, z, t) = y(x, y, z)exp[- i (E / h) t ]

. (85.4)

Тут E – повна енергія частинки, яка у випадку стаціонарного поля залишається сталою. Щоб переконатися у справедливості виразу (85.4), підставимо його в рівняння (85.1). У результаті цього отримаємо співвідношення

- h exp[- i (E / h) t ] Dy + U y exp[- i (E / h) t ]

= i h[- i (E / h)]y exp[- i (E / h) t ].

2 m

Скоротивши на загальний множник exp[- i (E / h) t ], прийдемо до диференціального рівняння, що визначає функцію y:

- h Dy + U y = E y. (85.5)

2 m

Рівняння (85.5) називається рівнянням Шредінгера для стаціонарних станів (стаціонарне рівняння Шредінгера). Надалі ми будемо мати справу тільки із цим рівнянням і для стислості будемо називати його просто рівнянням Шредінгера. Рівняння (85.5) часто пишуть у вигляді

Dy + 2 m (E - U)y = 0. (85.6)

h

У випадку стаціонарного силового поля хвильова функція має вигляд (85.4). Тоді

Y*Y = exp[ i (E / h) t ]y*× exp[- i (E / h) t ]y = y*y.

Таким чином, густина імовірності дорівнює

y*y

й, отже, від часу не залежить. Саме тому

стани, які описуються хвильовими функціями вигляду (85.4), називають стаціонарними.

3 У класичній механіці стан частинки (матеріальної точки) визначається заданням положення і швидкості (або імпульсу) частинки. Якщо є відомим стан у початковий момент часу й силове поле, у якому знаходиться частинка, то, розв’язавши рівняння Ньютона, можна знайти положення й швидкість частинки у будь-який наступний момент часу. У цьому полягає сутність причинності в класичній механіці.

У квантовій механіці класичне поняття стану позбавлене змісту, тому що координата

й швидкість частинки принципово не можуть мати одночасно певних значень. Тому класичне поняття причинності також не можна застосовувати у квантовій теорії. Стан частинки задається у квантовій механіці хвильовою функцією. Якщо відомі хвильова функція в початковий момент часу й силове поле, у якому рухається частинка, то, розв’язавши рівняння Шредінгера, можна знайти хвильову функцію в наступні моменти часу. У цьому полягає сутність причинності у квантовій механіці. Таким чином, квантова механіка не скасувала принцип причинності. Вона лише надала йому форму, яка відповідає дійсній природі речей.

§ 86 Рівняння Шредінгера та квантування енергії [6]

1 Квантування енергії виникає тому, що на хвильові функції y, які є розв’язками рівняння Шредінгера

- h Dy + U y = E y, (86.1)

2 m

накладаються певні обмеження – стандартні умови для хвильової функції. При цих обмеженнях рівняння (86.1) має розв’язки, у загальному випадку, не при всіх, а тільки при вибраних значеннях параметра E (E визначає енергію частинки). Тут маємо випадок, аналогічний до того, що має місце в задачі про вільні коливання струни із закріпленими кінцями. Через закріпленість кінців ці коливання є стоячими хвилями з такими вибраними частотами, що на довжині струни вкладається ціле число напівхвиль.

Стандартні умови для хвильової функції, що накладаються на розв’язки рівняння

Шредінгера, полягають у тому, що хвильова функція

y(x, y, z)

і її перші просторові похідні

повинні бути скінченними, однозначними й неперервними, інтеграл від

y(x, y, z) по усьому

простору повинен бути скінченним. Вибрані значення параметра E, для яких рівняння Шредінгера має розв’язки, що задовольняють стандартні умови, називаються власними значеннями величини E для диференціального рівняння (86.1), а відповідні їм розв’язки – власними функціями того самого рівняння. Власні значення E і беруть за можливі значення енергії у стаціонарних станах. Власні значення енергії E можуть бути дискретними, а можуть неперервно заповнювати скінченний або нескінченний інтервал. У першому випадку говорять, що енергетичний спектр дискретний, а в другому – неперервний.

Таким чином, квантування енергії випливає з основних положень квантової механіки без будь-яких додаткових припущень.

§ 87 Частинка в одновимірній потенціальній ямі. Енергія і хвильова функція частинки в потенціальній ямі [6]

1 У нерелятивістській квантовій механіці основним принципом є рівняння Шредінгера. Пошук розв’язків цього рівняння, які задовольняють стандартні умови, приводить до дискретності енергетичних рівнів. Продемонструємо це на прикладі задачі про частинку, яка знаходиться в одновимірній нескінченно глибокій потенціальній ямі.

Знайдемо власні значення енергії й відповідні їм власні функції для частинки, що

знаходиться в нескінченно глибокій одновимірній потенціальній ямі. Припустимо, що частинка може рухатися тільки уздовж осі X. Нехай рух обмежений непроникними для

частинки стінками з такими координатами:

x = 0 і

x = l. Потенціальна енергія U має в

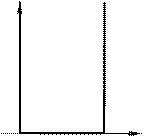
цьому випадку такий вигляд (рис. 87.1 а): вона дорівнює нулю при 0 £ x £ l

й перетворюється

у нескінченність при рівняння Шредінгера

x < 0 й

x > l. Для розв’язання задачі використаємо стаціонарне

Dy + 2 m (E - U)y = 0. (87.1)

U

U = ¥

h

n = 4

    n = 3

  n = 2

n = 1

E 4

U = ¥ E

E 2 E 1

0 l x 0

a б

Рисунок 87.1: а – нескінченно глибока потенціальна яма; б –

схема рівнів енергії частинки, що знаходиться в такій ямі

2 Оскільки хвильова функція залежить тільки від координати x, то рівняння (87.1)

спрощується:

¶ y + 2 m (E - U)y = 0. (87.2)

¶ x 2 h2

За межі потенціальної ями частинка потрапити не може (там потенціальна енергія

дорівнює нескінченності

U = ¥). Тому ймовірність виявлення частинки за межами ями

дорівнює нулю. Відповідно й функція y за межами ями дорівнює нулю. З умови

неперервності випливає, що y повинна дорівнювати нулю й на межах ями, тобто

y(0) = y(l) = 0. (87.3)

Це і є одна із стандартних умов, яку повинен задовольняти розв’язок рівняння (87.2). В області, де y не дорівнює тотожно нулю, рівняння (87.2) має вигляд

¶ y + 2 mE y = 0

(87.4)

¶ x 2 h2

(у цій області U = 0). Увівши позначення

k 2 = 2 mE, (87.5)

прийдемо до рівняння

h

y¢¢+ k 2y = 0,

яке в теорії коливань називають диференціальним рівнянням гармонічних коливань. Розв’язок такого рівняння має вигляд

y(x) = A sin(kx + a)

(87.6)

(у цьому випадку зручніше взяти синус замість косинуса). Умови (87.3) можна задовольнити

відповідним вибором сталих k і a. Насамперед з умови y(0) = 0

y(0) = A sin a = 0,

отримуємо

звідки випливає, що a повинна дорівнювати нулю. Також повинна виконуватися умова

y(l) = A sin (kl) = 0,

що можливо лише у випадку, коли

kl = ± n p

(n = 1, 2, 3,...)

(87.7)

(n = 0

не беремо до уваги, оскільки при цьому виходить, що

y = 0

– частинка у

потенціальній ямі відсутня).

Виключивши k з рівнянь (87.5) і (87.7), знайдемо власні значення енергії частинки:

E = E

h

p2 2 2

= n

(n = 1, 2, 3,...). (87.8)

n 2 ml 2

Спектр енергії виявився дискретним. На рис. 87.1 б зображена схема енергетичних рівнів.

Відповідно до формули (87.8) мінімальна енергія, яку може мати частинка, що знаходиться в потенціальній ямі, відмінна від нуля. Цей результат обумовлений хвильовими

властивостями частинки й може бути отриманий зі співвідношення невизначеностей.

3 Далі знайдемо власну хвильову функцію рівняння Шредінгера. Підставивши в (87.6)

значення k, яке отримали з умови (87.7), знайдемо власні хвильові функції:

y = y n

(x) = A sin n p x

l

(нагадаємо, що

a = 0). Для знаходження коефіцієнта A використаємо умову нормування,

яку у цьому випадку запишемо так:

l

A 2òsin 2 0

n p x l

dx = 1.

Нескладно отримати, що

l l l

ò 2 n p x

1 - cos(2 n p x / l)

= ò

= æ x - sin (2 n p x / l) ö

l.

sin dx

l

0 0

dx ç

2 è2

2 × (2 n p / l)

÷ =

ø 0 2

Звідси

A 2× l / 2 = 1, або A =

2 / l. Таким чином, власні функції частинки в потенціальній

ямі мають вигляд

y (x) =

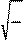2 sin n p x

(n = 1, 2, 3,...). (87.9)

n l

y

n = 4

l

y*y

n = 4

n = 3

n = 3

n = 2

n = 1

0 l x

a

n = 2

n = 1

0 l x

б

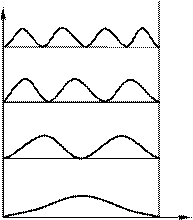
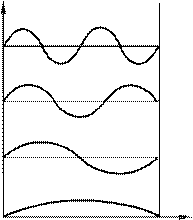
Рисунок 87.2: а – графіки власні функції частинки, що знаходиться в потенціальній ямі, яка зображена на рис. 87.1 а; б – густина ймовірності знаходження частинки в точках з різними значеннями координати x

Графіки власних функцій зображені на рис. 87.2 а. На рис. 87.2 б подана густина

ймовірності виявлення частинки на різних відстанях від стінок ями, що дорівнює

y*y. Із

графіків, наприклад, випливає, що в стані із

n = 2

частинка не може бути виявлена всередині

ями й разом з цим однаково часто буває як у лівій, так і в правій половині ями. Така

поведінка частинки є несумісною з класичними уявленнями про траєкторії. Відзначимо, що відповідно до класичних уявлень усі положення частинки в ямі мають однакову ймовірність.

§ 88 Тунельний ефект. Коефіцієнт проходження [3]

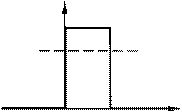
1 Нехай частинка, яка рухається зліва направо, зустрічає на своєму шляху

потенціальний бар'єр висотою U 0

й шириною l (рис. 88.1). За класичними уявленнями

частинка повинна вести себе так. Якщо енергія частинки більша за висоту бар'єра (E > U 0),

частинка безперешкодно проходить над бар'єром (на ділянці

0 £ x £ l

лише зменшується

швидкість частинки, але потім при

x > l

знову набуде початкового значення). Якщо ж E

менше U 0

(як зображено на рисунку), то частинка відбивається від бар'єра й летить у

зворотній бік; крізь бар'єр частинка проникнути не може.

Зовсім інакше виглядає поведінка частинки з точки зору

U (x)

до квантової механіки. По-перше, навіть при

E > U 0

є відмінна

U

від нуля ймовірність того, що частинка відіб'ється від бар'єра й 0

E

полетить у зворотній бік. По-друге, при

E < U 0

є відмінна від

нуля ймовірність того, що частинка проникне «крізь» бар'єр і

I II III

опиниться в області, де

x > l. Така поведінка є цілком

неможливою з	класичної точки зору.	Ця	поведінка		l
мікрочастинки Шредінгера.	випливає безпосередньо	з	рівняння Рисунок 88.1

x

2 Розглянемо випадок E < U 0. Рівняння Шредінгера має вигляд

d y + 2 mE y = 0

(88.1)

для областей I і III й

dx 2 h2

d y + 2 m (E - U

)y = 0

(88.2)

dx 2 h2 0

для області II, причому E - U 0< 0.

Будемо шукати розв'язок рівняння (88.1) у вигляді y = e l x. Підстановка цієї функції в

(88.1) приводить до характеристичного рівняння

l2+ 2 mE = 0.

Звідси l = ± i a, де

h

a = 1

h

2 mE. (88.3)

Таким чином, загальний розв'язок рівняння (88.1) має вигляд

y = A ei a x + B e - i a x

для області I,

1 1 1

y = A ei a x + B e - i a x

для області III. (88.4)

Вирішивши підстановкою цього рівняння у вигляді

y = e b x

рівняння (88.2), отримаємо загальний розв'язок

y = A e b x + B e -b x для області II. (88.5)

Тут

2 2

b = 1

h

2 m (U 0

- E). (88.6)

Зазначимо, розв'язок вигляду

ei a x

відповідає хвилі, яка поширюється в додатному

напрямку осі X, а розв'язок вигляду

e - i a x

– хвилі, яка поширюється в протилежному

напрямку. Щоб це зрозуміти, згадаємо, що звичайна (звукова, електромагнітна і т.п.) плоска

хвиля, яка поширюється в напрямку зростання x, описується дійсною частиною виразу ei (w t - kx), а хвиля, яка поширюється в напрямку зменшення x, – дійсною частиною виразу ei (w t + kx). Частинці, яка рухається в додатному напрямку осі X, зіставляється функція Y = ae (i / h)(px - Et). Якщо відкинути в цій функції часовий множник, то для y отримаємо вираз y = aei (p / h) x. Для частинки, яка рухається в протилежному напрямку, буде y = ae - i (p / h) x.

В області III є тільки хвиля, яка пройшла через бар'єр і поширюється зліва направо.

Тому коефіцієнт B 3

у виразі (88.4) для

y3потрібно покласти таким, що дорівнює нулю. Для

знаходження інших коефіцієнтів скористаємося стандартними умовами, які повинна задовольняти хвильова функція y. Для того щоб y була безперервною у всій області x від

- ¥ до

+ ¥, повинні виконуватися умови

y1(0) = y2(0)

і y2(l) = y3(l). Для того щоб y

була гладкою, тобто не мала зломів, повинні виконуватися умови

y¢2 (l) = y¢3 (l). Із цих умов випливають співвідношення:

A 1+ B 1= A 2+ B 2,

A e b l + B e -b l = A ei a l

y1¢ (0) = y¢2 (0) і

2 2 3,

i a A 1 - i a B 1 = b A 2 - b B 2,

(88.7)

b A e b l - b B e -b l = iaA ei a l

2 2 3.

Розділимо всі рівняння на

A 1й введемо позначення:

а також

b 1=

B 1,

A 1

a 2 =

A 2,

A 1

b 2=

B 2,

A 1

a 3 =

A 3,

A 1

Тоді рівняння (88.7) наберуть вигляду

n = b = a

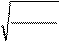U 0- E. (88.8)

E

1+ b 1= a 2+ b 2,

b l

a 2 e

+ b 2 e

-b l

= a 3 e

i a l,

(88.9)

i - ib 1= na 2- nb 2,

b l

na 2 e

- nb 2 e

-b l

= ia 3 e

i a l.

Відношення квадратів модулів амплітуд відбитої й падаючої хвилі

2

R = B 1

A 1

= b 1

визначає ймовірність відбиття частинки від потенціального бар'єра й називається

коефіцієнтом відбиття.

Відношення квадратів модулів амплітуд хвилі, що пройшла, й падаючої хвилі

2

D = A 3

A 1

= a 3

(88.10)

визначає ймовірність проходження частинки через бар'єр і називається коефіцієнтом проходження (або коефіцієнтом прозорості).

Нас буде цікавити тільки проходження частинок через бар'єр, і ми обмежимося

знаходженням величини D. Слід зазначити, знайшовши D, легко знайти R, оскільки ці

коефіцієнти пов'язані очевидним співвідношенням

R + D = 1.

Помножимо перше з рівнянь (88.9) на i й складемо з третім. У результаті отримаємо

2 i = (n + i) a 2- (n - i) b 2. (88.11)

Тепер помножимо друге з рівнянь (88.9) на i й віднімемо його від четвертого. Отримаємо:

(n - i) e b l

a 2 - (n + i) e

-b l

b 2= 0. (88.12)

Вирішивши спільно рівняння (88.11) і (88.12), знайдемо, що

-b l

a = 2 i (n + i ) e,

2 (n + i)2 e -b l - (n - i)2 e b l

2 i (n - i ) e b l

b =.

2 (n + i)2 e -b l - (n - i)2 e b l

Нарешті, підставивши знайдені нами значення a 2

вираз для a 3:

й b 2

у друге з рівнянь (88.9), отримаємо

+ - -

a 4 ni

- i a l.

Величина

3 = 2 -b l 2 b l e

(n i) e (n i) e

b l =

2 m (U 0 - E) l,

h

як правило, є набагато більшою за одиницю. Тому в знаменнику виразу для a 3

доданком,

який містить множник

e -b l, можна знехтувати у порівнянні з доданком, який містить

множник

e b l

(комплексні числа

n + i

й n - i

мають однаковий модуль). Отже, можна

припустити

a» - 4 nie

- i a l

e -b l.

3 (n - i)2

Згідно з (88.10) квадрат модуля цієї величини дає ймовірність проходження частинки через

потенціальний бар'єр. Урахувавши, що | n - i |=

n 2+ 1, отримаємо

D = a 2»

16 n 2

e -2b l,

3 (n 2 + 1)2

де

n 2= U 0- E = U 0-1

E E

(див. формулу (88.8)).

Вираз 16 n 2/(n 2+ 1)2

має величину порядку одиниці. Тому можна вважати, що

D» e -2b l = expé- 2 × l

2 m (U

- E)ù. (88.13)

ê h

0 úû

З отриманого нами виразу випливає, що ймовірність проходження частинки через потенціальний бар'єр істотно

U (x)

залежить від ширини бар'єра l й від величини

U 0 - E.

Якщо при якійсь ширині бар'єра коефіцієнт проходження D дорівнює, припустимо, 0,01, то при збільшенні ширини у два рази D буде дорівнювати 0,012 = 0,0001, тобто зменшується в 100 разів. Той самий

ефект у цьому випадку викликало б зростання в чотири

E

0 a b x

рази величини

U 0- E. Коефіцієнт проходження різко

Рисунок 88.2

зменшується при збільшенні маси частинки m.

3 Подібний розрахунок можна виконати у випадку потенціального бар'єра довільної форми (рис. 88.2). У цьому разі формула (88.13) повинна бути замінена більше загальною:

де U = U (x).

D» expé- 2 b

ê

ò

ë h a

2 m (U - E) dx ù, (88.14)

ú

û

При подоланні потенціального бар'єра частинка ніби проходить через «тунель» у цьому бар'єрі (див. заштриховану область на рис. 88.2). У зв'язку з цим розглянуте нами явище називають тунельним ефектом.

§ 89 Оператори фізичних величин. Власні функції та власні значення. Принцип суперпозиції [6]

Операторний метод широко використовується у більшості досліджень з квантової механіки. Розглянемо сутність цього методу.

1 Оператори. У квантовій механіці кожній фізичній величині ставиться у відповідність оператор. Під оператором мається на увазі правило, за допомогою якого одній функції (позначимо її через j ) зіставляється інша функція (позначимо її через f).

Символічно це записується так:

f = Q ˆj. (89.1)

Тут Q ˆ – позначення оператора. Для того щоб відрізнити оператори від чисел, їх позначають через Q ˆ, тобто ставлять кришечку над Q або використовують інше позначення.

Таким чином, під символом оператора розуміють сукупність дій, за допомогою яких вихідна функція (j) перетворюється в іншу функцію (f).

Наприклад, символ оператора Лапласа

D = Q ˆ1

позначає дворазове частинне

диференціювання за усіма трьома координатами x, y і z з подальшим підсумовуванням отриманих виразів. Тобто оператор Лапласа можна подати у вигляді

D = ˆ

= ¶ + ¶

+ ¶.

Q

1 ¶ x 2

¶ y 2

¶ z 2

За допомогою оператора можемо подати множення вихідної функції j на деяку

функцію U. Тоді наступне перетворення

Q ˆ2 = U.

f = U × j

можна записати у вигляді

f = Q ˆ2j, де

Використовуючи операторний підхід, рівняння Шредінгера

- h

2 m

можна записати в операторному вигляді

Dy + U y = E y

(89.2)

H ˆy = E y. (89.3)

У цьому рівнянні символом H ˆ позначений оператор, який дорівнює

H ˆ = - h

2 m

D + U. (89.4)

Цей оператор називають гамільтоніаном, або оператором Гамільтона. Гамільтоніан є оператором енергії E.

2 Сутність операторного методу. У квантовій механіці кожній фізичній величині

ставиться у відповідність оператор. Розглядаються оператори координат, імпульсу, моменту імпульсу і т.д. Для кожної фізичної величини q складається рівняння, аналогічне до рівняння Шредінгера в операторному вигляді (89.3). Воно має вигляд

Q ˆy = q y, (89.5)

де Q ˆ – оператор, який ставиться у відповідність фізичній величині q.

Значення q, при яких розв’язок рівняння (89.5) задовольняє стандартні умови для хвильової функції, називаються власними значеннями величини q, а самі розв’язки – її власними функціями. Власні значення величини q і беруться за можливі значення цієї величини, які спостерігаються в експерименті.

Розглядаючи з цих позицій рівняння Шредінгера (89.3), можемо стверджувати, що

воно є рівнянням для власних значень енергії (q = E). Оператор енергії визначається

співвідношенням (89.4) (Q ˆ = H ˆ).

3 Принцип суперпозиції. Спектр власних значень може бути як дискретним, так і суцільним. У випадку дискретного спектра власні значення й власні функції можна пронумерувати:

q 1, q 2,..., qn,...,

y1, y2,..., y n,...

(89.6)

За умови дискретного спектра власних значень фізичної величини спостерігаємо дві ситуації. Можливі стани, для яких при вимірюванні деякої величини q завжди отримуємо

однакові значення

qn. Про такі стани говорять як про стани, у яких величина q має певне

значення. Цей стан описується функцією

y n. Однак можливі також стани, для яких при

вимірюваннях отримуємо з різною ймовірністю різні власні значення оператора Q ˆ. Про такі стани говорять як про стани, у яких величина q не має певного значення.

Хвильова функція стану, у якому q не має певного значення, є суперпозицією

(накладенням) власних функцій величини q:

y = å cn y nn

, (89.7)

де cn, у загальному випадку, є комплексними числами, які не залежать від координат.

Кількість доданків у сумі дорівнює числу різних власних функцій величини q.

Формула (89.7) виражає принцип суперпозиції хвильових функцій: коли хвильові

функції

y1, y2,..., y n,...

описують деякі стани, то і функція

y = c 1y1+ c 2y2+... + cn y n +...

подає деяку хвильову функцію, що описує деякий стан системи. Обґрунтуванням принципу суперпозиції є узгодженість з дослідом наслідків, які випливають з нього. Так, за допомогою принципу суперпозиції квантова механіка пояснює дифракцію та інтерференцію частинок.

Квадрати модулів коефіцієнтів

cn дорівнюють імовірності того, що при вимірах, які

виконуються над системою, що перебуває у стані y, будуть отримані відповідні значення величини q. Оскільки сума всіх таких ймовірностей повинна дорівнювати одиниці,

коефіцієнти cn

задовольняють умову

å cn n

= 1.

§ 90 Середні значення фізичних величин з точки зору операторного підходу. Оператори радіуса-вектора, імпульсу, енергії. Зв'язок між власними й середніми значеннями [11]

1 Як визначають середнє значення фізичної величини в квантовій механіці, використовуючи операторний підхід? Для відповіді на це питання розглянемо приклад. Припустимо, що багаторазово проводиться вимір координати x частинки, причому частинка кожного разу перебуває в однакових макроскопічних умовах. Тоді стан частинки в цих

дослідах можна характеризувати хвильовою функцією

y(x), яку для спрощення будемо

вважати функцією тільки однієї просторової координати x. Середнє значення координати, яке буде знайдено в результаті вимірів, можна записати у вигляді

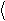
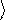
x = ò xdP = ò x y*y dx = ò y* x y dx. (90.1)

Тут використано, що

dP = y 2 dV = y*y dx

є, виходячи з фізичного змісту квадрата модуля

хвильової функції, ймовірністю того, що частинка буде знайдена в інтервалі

x, x + dx.

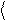
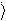Використовуючи операторний підхід, вираз для середнього значення x записують інакше:

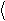
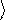x = ò y* x ˆy dx, (90.2)

де x ˆ оператор величини x. Порівнюючи вирази (90.1) і (90.2), бачимо, що оператор x -й координати має вигляд

x ˆ = x.		(90.3)
Аналогічно можна показати, що оператори	y йz -координат	виражаються

формулами

y ˆ = y,

z ˆ = z. (90.4)

Таким чином, оператор радіуса-вектора можна записати в так:

...

....

r ˆ = ex x ˆ + ey y ˆ + ez z ˆ = ex x + ey y + ez z =.. (90.5)

Абсолютно так само обчислюється середнє значення довільної функції від координат

f (x, y, z):

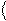
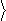f (x, y, z)

= ò y* f ˆy dxdydz, (90.6)

де оператор функції

f (x, y, z) знаходять так, як і оператор радіуса-вектора (див. (90.5)):

f ˆ = f (x ˆ, y ˆ, z ˆ) =

f (x, y, z). (90.7)

Вищевикладений метод знаходження середніх значень поширюють у квантовій механіці на будь-яку фізичну величину (яка залежить не тільки від координат, а й від

імпульсів). Для будь-якої фізичної величини F (r, p)

середнє значення визначається як

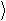F = òy* F ˆy dV

, (90.9)

де F ˆ – оператор величини F (r, p), який має вигляд

F ˆ = F (r. ˆ, p. ˆ). (90.10)

2 Знайдемо в явному вигляді оператор імпульсу.

Як відомо, енергія частинки дорівнює сумі кінетичної та потенціальної енергії і визначається функцією

H (., p.) =

p + U (x, y, z). (90.11)

2 m

Використовуючи правило (90.10), енергії (90.11) можна поставити у відповідність оператор

H ˆ = H (p ˆ, r ˆ)= (p ˆ)

+ U (x ˆ, y ˆ, z ˆ) = (p ˆ)

+ U (x, y, z). (90.12)

... 2. 2

2 m 2 m

Порівняємо оператор (90.12) з оператором Гамільтона (оператор енергії, який визначили з рівняння Шредінгера)

H ˆ = - h

D + U (x, y, z). (90.13)

2 m

З порівняння (90.12) та (90.13) випливає

(p. ˆ)2

2 m

= - h

2 m

D º - h

2 m

(.)2

(- i Ñ)2

Ñ

.

h

º.

2 m

.

Тут використали зв’язок між оператором Лапласа D та оператором набла Ñ:

порівняння знаходимо, що оператор імпульсу має вигляд

D = (.)2. З

Ñ

.ˆ.

æ. ¶

. ¶

. ¶ ö

p = - i hÑ º - i hç ex

è

¶ x + ey

¶ y + ez

÷. (90.14)

¶ z ø

Зрозуміло, що оператор енергії визначається співвідношенням (90.13).

3 З’ясуємо, як пов’язані між собою середні значення, що визначаються способом

та власні значення фізичних величин.

Для спрощення математичних перетворень розглянемо випадок стану системи, у яких

величина q має певне значення. Це означає, що цей стан описується хвильовою функцією

y = y n, яка відповідає власному значенню задовольняють рівнянню

qn. Хвильова функція y n

і власне значення qn

Q ˆy n = qn y n, (90.15)

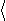
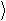де Q ˆ – оператор величини q. Середнє значення величини q в цьому випадку відповідає

власному значенню, тобто

q = qn.

З іншого боку, середнє значення можемо також визначити у спосіб (90.9). Тому

*

q = òy nQ ˆy n dV.

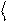
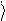
Використаємо в цьому співвідношенні рівняння (90.15) і отримаємо

* *

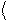
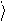q = òy nqn y ndV = qn ò y n y ndV = qn. (90.16)

Тут використали, що власне значення qn

не залежить від координат, а також умову

нормування для хвильової функції

òy* y

ndV = 1.

n

Таким чином, середні значення, що визначаються способом (90.9) та за допомогою

власних значень, мають одне і те саме значення.

§ 91 Комутативність операторів. Умови, за яких дві фізичні величини можуть бути виміряні одночасно [11]

1 Розглянемо дві фізичні величини a та b, яким відповідають оператори A ˆ та B ˆ. Чи завжди існує стан y, у якому обидва оператори мають визначені власні значення a та b? Тобто, чи завжди хвильова функція y є власною функцією одночасно як для оператора A ˆ, так і для оператора B ˆ? Іншими словами, чи можливо обидві фізичні величини a та b точно виміряти одночасно?

Для відповіді на це питання припустимо, що y є власною функцією як оператора A ˆ,

так і оператора B ˆ. Тобто

A ˆ y = a y,

B ˆy = b y,

де a й b – власні значення операторів A ˆ і B ˆ в стані, якому відповідає одна і та сама хвильова функція y. Помножимо першу рівність на оператор B ˆ. Отримаємо

B ˆ A ˆ y = B ˆ a y = aB ˆy = a × b × y.

Аналогічно

Звідси випливає, що

A ˆ B ˆy = A ˆ b y = bA ˆ y = b × a × y.

або

(A ˆ B ˆ - B ˆ A ˆ)y = 0,

A ˆ B ˆ = B ˆ A ˆ. (91.1)

Оператори, які мають властивість (91.1), називають комутативними.

Отже, якщо всі власні функції операторів A ˆ і B ˆ збігаються, то ці оператори комутують між собою. Справедлива й зворотна теорема: якщо оператори A ˆ й B ˆ комутують між собою, то збігаються і їх власні функції.

Наведеній теоремі можна надати й інше формулювання. Дві величини a й b можна виміряти одночасно, тоді й тільки тоді, коли відповідні їм оператори A ˆ й B ˆ комутують між собою.

2 Розглянемо приклади. Так координату x й відповідний їй імпульс

px одночасно

виміряти неможливо, оскільки оператори x ˆ й Переконаємося у цьому. Як відомо,

p ˆ x

не є комутативними між собою.

Тоді

x ˆ = x,

p ˆ x = - i h¶ / ¶ x.

æ ¶ ¶ ö æ ¶ ¶ ö

(p ˆ x x ˆ - x ˆ p ˆ x)y =- i hç

× x - x ×

÷y =- i hç

(x × y)- x ×

y ÷ =

è ¶ x

æ ¶

¶ x ø

¶

è¶ x

ö

¶ x ø

= - i hç y + x ×

è ¶ x

y - x ×

¶ x

y ÷ = - i hy ¹ 0.

ø

Тобто

p ˆ x x ˆ ¹ x ˆ p ˆ x, оператори x ˆ й

p ˆ x

не комутують між собою. Звідси випливає, що

одночасно точно визначити координату x та її проекцію імпульсу твердження узгоджується з принципом невизначеностей Гейзенберга.

px неможливо. Це

Аналогічно можна впевнитись в тому, що координати x й y можна виміряти

одночасно, тому що оператори x ˆ й y ˆ комутують.

§ 92 Квантування моменту імпульсу. Модуль і одна з проекцій моменту імпульсу. Азимутальне і магнітне квантові числа [6]

.

1 Момент імпульсу частинки L

визначається векторним добутком

відносно початку координат O у класичній механіці

.

L = [. ´ p. ]=

...

e

e

e

x y z

x y z px py pz

.

. (92.1)

У квантовій механіці моменту імпульсу частинки L

відповідає оператор

.ˆ

L = [ r. ˆ ´ p. ˆ ]=

.

e

Дата добавления: 2014-01-11