Розділ 5 елементи атомної фізики та квантової механіки

ТЕМА 13 БОРІВСЬКА ТЕОРІЯ АТОМА

§ 76 Дослід Резерфорда. Ядерна модель атома. Залежність кількості α-частинок в одиниці тілесного кута від кута розсіяння. Проблема стабільності атома з точки зору ядерної моделі атома [6]

1 Дослід Резерфорда. Цікавість людини є безмежною. Яка внутрішня структура атома

– найдрібнішої частинки хімічного елемента? Атом є електрично нейтральним, як усередині атома розподілені додатні та від’ємні електричні заряди? Відповіді на ці питання шукали Резерфорд і його співробітники за допомогою a -частинок, спостерігаючи зміну напрямку їх польоту (розсіювання), при проходженні через тонкі шари речовини.

У той час, коли Резерфорд приступав до своїх дослідів, було відомо, що a -частинки випромінюються деякими речовинами при радіоактивному розпаді. Швидкості a -частинок

мають порядок

м/с. Вони мають додатний заряд, що дорівнює подвоєному

елементарному заряду. При втраті цього заряду (при приєднанні двох електронів)

a -частинка перетворюється в атом гелію.

Дослід виконувався так (рис. 76.1). M a -частинки випромінювалися радіоактивною E речовиною Р, проходили через вузький отвір і P

попадали на тонку металеву фольгу Ф. При q

проходженні через фольгу a -частинки

відхилялися від початкового напрямку руху на Ф

різні кути. Розсіяні a -частинки вдарялися об екран Е, який був покритий сірчистим цинком, і

викликане ударами світіння спостерігалися в мікроскоп М. Мікроскоп і екран можна було

обертати навколо осі, що проходить через центр

Рисунок 76.1 – Схема досліду Резер- форда

розсіювальної фольги, і встановлювати під будь-яким кутом q. Весь прилад розміщувався у посудині, з якої було відкачано повітря. Це було зроблено для того, щоб усунути розсіювання a -частинок за рахунок зіткнень із молекулами повітря.

2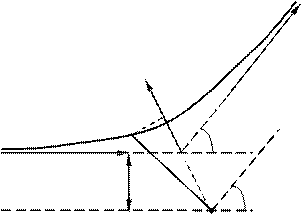

p

Ядерна модель атома. Виявилося, що деяка кількість a -частинок розсіюється на дуже великі кути (майже до 180°). Проаналізувавши результати досліду, Резерфорд дійшов висновку, що настільки сильне відхилення a -частинок можливо тільки в тому випадку, коли усередині атома є надзвичайно сильне електричне поле, що створюється зарядом,. який пов'язаний з великою масою й 0

сконцентрований у дуже малому об'ємі. Ґрунтуючись на цьому висновку,

p

D p a(+ 2 e)

q

b r

q

Резерфорд запропонував у 1911 р. ядерну модель атома. Відповідно до Резерфорда

атом являє собою систему зарядів, у

Рисунок 76.2

Ядро(+Ze)

центрі якої розміщене важке додатне ядро із зарядом Ze із розміром не більше 10-14 м, а навколо ядра розміщені Z електронів, що розподілені в усьому об'ємі атому. Майже вся маса атома зосереджена в ядрі.

3 Залежність кількості α-частинок в одиниці тілесного кута від кута розсіяння. Виходячи з таких припущень, Резерфорд розробив кількісну теорію розсіювання a -частинок і довів формулу для розподілу розсіяних частинок залежно від кута q. При доведенні формули Резерфорд міркував так. Відхилення a -частинок обумовлені впливом на них атомних ядер. Помітного відхилення через взаємодію з електронами не може бути, оскільки маса електрона на чотири порядки менша від маси a -частинки.

Коли частинка пролітає поблизу ядра, на неї діє кулонівська сила відштовхування

1 2 Ze 2

F =. (76.1)

4pe0 r 2

У цьому випадку траєкторія частинки являє собою гіперболу. Кут між асимптотами гіперболи позначимо буквою q (рис. 76.2). Цей кут характеризує відхилення частинки від первісного напрямку. Відстань b від ядра до первісного напрямку польоту a -частинки називається прицільним параметром. Чим ближче пролітає частинка від ядра (чим менше b), тим, природно, сильніше вона відхиляється (тим більше q). Величини b і q пов’язані між собою співвідношенням

ctgq = 4pe0 m au

b, (76.2)

2 2 Ze 2

яке можна довести, використовуючи закон збереження повної механічної енергії та моменту імпульсу.

Розглянемо настільки тонкий шар d q

розсіювальної речовини, щоб кожна

частинка при проходженні через нього пролітала поблизу тільки одного ядра,

тобто щоб кожна частинка мала лише db q

однократне розсіювання. Для того щоб

частинка відхилилася на кут, що лежить у 2 b

межах від q до

q + d q, вона повинна

пролетіти поблизу одного з ядер по траєкторії, прицільний параметр якої

міститься у межах від b до

b + db

(рис. 76.3), причому db й

d q, як випливає

Рисунок 76.3

з (76.2), пов'язані співвідношенням

d q 4pe m u2

-

sin 2 (q / 2) 2

= 0 a

2 Ze 2

db. (76.3)

Знак мінус у цьому виразі обумовлений тим, що зі збільшенням b (тобто при

db > 0) кут

відхилення зменшується (d q < 0). Надалі нас буде цікавити лише абсолютне значення db у функції від q, і тому знак мінус ми не будемо враховувати.

Позначимо площу поперечного перерізу пучка a -частинок

буквою S. Тоді кількість атомів фольги на шляху пучка можна S db

подати у вигляді nSa, де n – число атомів в одиниці об'єму, a – b

товщина фольги. Якщо a -частинки розподілені рівномірно по перерізу пучка й число їх дуже велике (що насправді має місце),

то відносна кількість a -частинок, що пролітають поблизу одного

з ядер по траєкторії із прицільним параметром від b до

b + db

(і,

отже, які відхиляються в межах кутів від q до

q + d q), буде

дорівнювати відношенню відповідних площ (див. рис. 76.4):

Рисунок 76.4

dN q= nSa × 2p b db = na 2p bdb. (76.4)

N S

У цьому виразі

dN q

– потік частинок, що розсіюються в межах кутів від q до

q + d q, N –

повний потік частинок у пучку.

Замінивши у формулі (76.4) b і db через q і d q

отримаємо

відповідно до (76.2) і (76.3),

q =

dN æ

na ç

2 Ze 2

÷

ö 2p ctg q 1

d q. (76.5)

N ç 4pe m

u2÷

2 sin 2 (q / 2) 2

è 0 a ø

Перетворимо множники, що містять кут q:

ctg(q / 2)

=

sin 2 (q / 2)

З урахуванням цього перетворення

cos(q / 2) sin (q / 2)

=

sin 4 (q / 2)

sin q. 2sin 4 (q / 2)

q =

dN æ

na ç

2 Ze 2

ö 2p sin q d q

÷.

N ç 4pe m

u2÷

4 sin 4 (q / 2)

è 0 a ø

Вираз

2p sin q d q дає тілесний кут

d W, у межах якого знаходяться напрями, що відповідають

кутам розсіювання від q до q + d q. Тому можна написати

æ 2 2 ö W

dN q

na ç Ze ÷

d

N = ç 4pe m

u2÷

4 sin 4 (q / 2). (76.6)

è 0 a ø

Ми отримали формулу Резерфорда для розсіювання a -частинок. У 1913 р. співробітники Резерфорда зробили перевірку цієї формули шляхом підрахунку точок світіння на екрані, що спостерігалися під різними кутами q за однакові проміжки часу. В умовах досліду (див. рис. 76.1) враховувалися a -частинки, які перебували в межах одного і того самого тілесного кута (який визначається відношенням площі екрана Е до квадрата відстані його від фольги), тому число точок світіння, що спостерігалися під різними кутами,

повинне було бути, відповідно до формули Резерфорда, пропорційно

1/(sin(q / 2))4. Цей

результат теорії добре підтвердився на досліді. Залежність розсіювання від товщини фольги й швидкості a -частинок також виявилася узгодженою з формулою (76.6).

Справедливість теорії, що випливає із кулонівської взаємодії між a -частинкою і ядром атома, свідчить про те, що a -частинка, яка відбивається у зворотному напрямку, не проникає в область додатного заряду атома. Разом з тим a -частинка, що летить точно у

напрямку ядра, підійшла б до його центра на відстань, яку можна визначити, прирівнявши кінетичну енергію a -частинки до потенціальної енергії взаємодії a -частинки з ядром у момент повної зупинки частинки

m u2

2 Ze 2

a =

4pe0 r min

(r min

– мінімальна відстань між центрами a -частинки і ядра). Поклавши

Z = 47

(срібло),

u = 107

м/с і m a

= 6,6 ×1027

кг, отримаємо

4 Ze

-14

r min =

4pe m

» 6 ×10 м.

u2

0 a

4 Проблема стабільності атома з точки зору ядерної моделі атома. Отже, результати дослідів з розсіювання a -частинок свідчать на користь запропонованої Резерфордом ядерної моделі атома. Однак ядерна модель виявилася суперечливою відносно законів класичної механіки й електродинаміки. Оскільки система нерухомих зарядів не може перебувати в стійкому стані, то Резерфорду довелося відмовитися від статичної моделі атома

й припустити, що електрони рухаються навколо ядра, описуючи викривленні траєкторії. Але в цьому випадку електрон буде рухатися із прискоренням, у зв'язку із чим відповідно до класичної електродинаміки він повинен безперервно випромінювати електромагнітні (світлові) хвилі. Процес випромінювання супроводжується втратою енергії, так що електрон повинен в остаточному підсумку впасти на ядро.

§ 77 Постулати Бора. Правило квантування орбіт. Досліди Франка й Герца [6]

1 Постулати Бора. Правило квантування орбіт. У попередньому параграфі було з'ясовано, що ядерна модель атома з точки зору класичної механіки й електродинаміки виявилася нездатною пояснити стійкість атома. Вихід з цього утруднення був знайдений в 1913 р. датським фізиком Нільсом Бором, щоправда, ціною введення припущень, що суперечать класичним уявленням. Припущення, запропоновані Бором, містяться у двох сформульованих ним постулатах (постулати Бора).

1) Атом (і будь-яка атомна система) може перебувати не у всіх станах, що

допускаються класичною механікою, а тільки в деяких вибраних (квантових) станах, що

характеризуються певними перервними, дискретними значеннями енергії

E 1, E 2, E 3,... У цих

станах, всупереч класичній електродинаміці, атом не випромінює. Тому вони називаються стаціонарними станами.

2) Випромінювання випускається або поглинається у вигляді світлового кванта

енергії

hw при переході електрона з одного стаціонарного стану в інший. Величина

світлового кванта дорівнює різниці енергій стаціонарних станів, між якими відбувається квантовий перехід електрона:

hw = En - Em. (77.1)

Які ж орбіти потрібно вважати стаціонарними? На це питання відповідає правило квантування орбіт: у стаціонарному стані атома електрон, рухаючись по орбіті, повинен мати дискретні, квантовані значення моменту імпульсу:

L = me u r = n h (n = 1,2,3,...). (77.2)

Тут

me – маса електрона; u – його швидкість; r – радіус кругової орбіти; n – ціле число, що

з часом отримало назву головного квантового числа. Правило квантування орбіт Бор отримав, виходячи з гіпотези Планка, відповідно до якої реалізуються тільки такі стани

гармонічної коливальної системи (гармонічного осцилятора), енергія яких дорівнює

n hw¢, де

w¢– частота коливальної системи. Отримане правило для гармонічного осцилятора Бор поширив і на інші механічні системи.

Постулати Бора стали обґрунтуванням планетарної (ядерної) моделі атома, пояснили

ряд експериментів.

2 Досліди Франка й Герца. Існування

дискретних енергетичних рівнів атома підтверджується дослідами, виконаними в 1914 р. Франком і Герцом. Схема їх установки наведена на рис. 77.1. У трубці, яка заповнена парами ртуті під невеликим тиском (~1 мм рт. ст.), знаходяться три електроди: катод К, сітка С й анод А. Електрони, що вилітають з катода внаслідок термоелектронної емісії, прискорю- ються різницею потенціалів U, яка прикладена між катодом і сіткою. Цю різницю потенціалів можна плавно змінювати за допомогою

K C A

V G

П + –

– +

Рисунок 77.1

потенціометра П. Між сіткою й анодом створювалося слабке електричне поле (різниця потенціалів порядку 0,5 В), яке гальмувало рух електронів до анода. На рис. 77.2 показана

зміна потенціальної енергії електрона

E p = - e j

у зазорі між електродами при різних

значеннях напруги U між катодом і сіткою (j – потенціал, у відповідній точці поля).

Досліджувався струм I в колі анода залежно від напруги U між катодом і сіткою. Сила струму вимірялася гальванометром G, напруга – вольтметром V. Отримані результати подані на рис. 77.3. Бачимо, що сила струму спочатку монотонно зростала, досягаючи максимуму при U = 4,9 В, після чого з подальшим збільшенням U різко спадала, досягаючи мінімуму, і знову починала зростати. Максимуми сили струму повторювалися при напрузі U, що дорівнювала 9,8 В, 14,7 В і т.д.

Такий хід кривої пояснюється тим, що внаслідок

E p дискретності енергетичних рівнів атоми можуть поглинати U 3енергію тільки порціями: U 2

D E 1= E 2- E 1

або

D E 2= E 3- E 1

і так далі,

U

де E 1, E 2, E 3,... – енергія 1-го, 2-го й т.д. стаціонарних станів.

Поки енергія електрона менша за

D E 1, зіткнення між

електроном і атомом ртуті мають пружний характер, причому оскільки маса електрона набагато менша від маси атома ртуті,

енергія електрона при зіткненнях практично не змінюється. Частина електронів попадає на сітку, інші ж, проскочивши

K C A

Рисунок 77.2

через сітку, досягають анода, створюючи струм у колі гальванометра G. Чим більша швидкість, з якої електрони досягають сітки (чим більше U), тим більше буде електронів, які проскочили через сітку, і, отже, тим більшою буде сила струму I.

Коли енергія, що отримується електроном у I

проміжку катод-сітка, досягає значення

D E 1, зіткнення

перестають бути пружними – електрони при ударах об

атоми передають їм енергію

D E 1

й продовжують потім

рухатися з меншою швидкістю. Тому число електронів, що

досягають анода, зменшується. Наприклад, при

U = 5,3 В

електрон передає атому енергію, що відповідає 4,9 В

(перший потенціал збудження атома ртуті), і продовжує рухатися з енергією 0,4 еВ. Якщо навіть такий електрон з’явиться між сіткою й анодом, він не зможе перебороти затримуючу напругу 0,5 В і буде повернутий назад на сітку.

Атоми, що отримали при зіткненні з електронами

0 4,9 9,8 14,7

Рисунок 77.3

U, B

-8

енергію

D E 1, переходять у збуджений стан, з якого вони через час порядку 10 с

повертаються в основний стан, випромінюючи фотон із частотою w = D E 1/ h.

При напрузі, що перевищує 9,8 В, електрон на шляху катод-анод може двічі перетерпіти непружне зіткнення з атомами ртуті, втрачаючи при цьому енергію 9,8 еВ,

внаслідок чого сила струму I знову почне зменшуватися. При ще більшій напрузі можливі

трикратні непружні зіткнення електронів з атомами, що приводить до виникнення максимуму при U = 14,7 В, і т.д.

При достатньому розрідженні парів ртуті й відповідній величині прискорювальної

напруги електрони за час до зіткнення з атомами можуть отримати швидкість, достатню для

переведення атома у стан з енергією

E 3. У цьому випадку на кривій

I = f (U)

будуть

спостерігатися максимуми при напругах, кратних другому потенціалу збудження атома (для ртуті цей потенціал дорівнює 6,7 В), або при напругах, що дорівнюють сумі першого й другого потенціалів збудження і т.д.

Таким чином, у дослідах Франка й Герца безпосередньо спостерігається існування в атомів дискретних енергетичних рівнів.

§ 78 Спектральні закономірності у випромінюванні атома водню. Терми. Комбінаційний принцип Рітца [6]

1 Випромінювання невзаємодіючих один з одним атомів складається з відокремлених спектральних ліній. Відповідно до цього спектр випромінювання атомів називається лінійчастим.

Вивчення атомних спектрів стало ключем до пізнання будови атомів. Насамперед було помічено, що лінії в спектрах атомів розміщені не безсистемно, а поєднуються в групи або, як їх називають, серії ліній. Краще всього це проявляється в спектрі найпростішого атома – водню. На рис. 78.1 подана частина спектра атомарного водню у видимій і близькій

ультрафіолетовій області. Символами

H a,

H b, H g

і H d

позначені видимі лінії.

H ¥ вказує

межу серії (див. нижче). Очевидно, що лінії розміщені у певному порядку. Відстань між лініями закономірно зменшується при переході від більш довгих хвиль до більш коротких.

Швейцарський фізик Бальмер (1885) виявив, що довжини хвиль цієї серії ліній водню можуть бути точно подані формулою

-

æ 1 1 ö

w = R ç ÷

è 22 n 2ø

(n = 3, 4, 5,...), (78.1)

де n – ціле число, що набуває значень 3, 4, 5 і т.д.; R – константа, названа на честь шведського спектроскопіста сталою Рідберга 1. Вона дорівнює

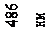
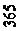R = 2,07 ×1016 c -1. (78.2)

Формула (78.1) називається формулою Бальмера 1, а відповідна серія спектральних ліній водневого атома – серією Бальмера. Подальші дослідження показали, що у спектрі водню є ще кілька серій. В ультрафіолетовій частині спектра

знаходиться серія Лаймана. Інші

серії лежать в інфрачервоній H a

області. Лінії цих серій можуть бути

H b H g H d H ¥

подані у вигляді формул,

аналогічних до (78.2):

серія Лаймана

-

w = R æ 1 1 ö

ç 2 2 ÷

Рисунок 78.1

(n = 2, 3, 4,...),

è 1 n ø

-

æ 1 1 ö

серія Пашена

w = R ç 2 2 ÷

(n = 4, 5, 6,...),

è 3 n ø

-

æ 1 1 ö

серія Брекета

w = R ç ÷

è 42 n 2ø

(n = 5, 6, 7,...),

1 У спектроскопії спектральні лінії характеризують не частотою, а величиною, яка обернена до довжини хвилі

1/ l = w /(2p c).

Формула Бальмера, що написана для цієї величини, має такий самий вигляд, як (78.1):

= R

1 æ 1

¢ç

l è 22

1 ö

- ÷

n 2 ø

(n = 3, 4, 5,...).

Стала Рідберга набуває у цьому випадку значення R ¢=

10973731,77 ± 0,83 м-1.

-

æ 1 1 ö

серія Пфунда

w = R ç ÷

è 52 n 2ø

(n = 6, 7, 8,...).

Частоти усіх ліній спектра водневого атома можна подати однією формулою

-

æ 1 1 ö

w = R ç

è m 2

2 ÷, (78.3)

n ø

де m має значення 1 для серії Лаймана, 2 – для серії Бальмера і т.д. Для заданого m число n

набуває всіх цілих значень, починаючи з

формулою Бальмера.

m + 1. Вираз (78.3) називають узагальненою

При зростанні n частота лінії в кожній серії прямує до граничного значення

R / m 2,

яке називається межею серії (на рис. 78.1 символом H ¥

2 Візьмемо ряд значень виразів T (n) = R / n 2:

позначена межа серії Бальмера).

R, R,

12 22

R,... 32

(78.4)

Частота будь-якої лінії спектра водню може бути подана у вигляді різниці двох чисел ряду

(78.4). Ці числа називають спектральними термами, або просто термами. Так, наприклад,

частота першої лінії серії Бальмера дорівнює

T (2) - T (3), другої лінії серії Пфунда

T (5) - T (7)

і т.д.

Вивчення спектрів інших атомів показало, що частоти ліній і в цьому випадку можуть бути подані у вигляді різниці двох термів:

w = T 1(m) - T 2(n). (78.5)

Формула (78.5) виражає основний закон спектроскопії, встановлений емпірично в 1908 р., який називається комбінаційним принципом Рітца. Принцип Рітца полягає у тому, що все різноманіття спектральних ліній атома може бути отримане шляхом попарних комбінацій набагато меншого числа величин, які називаються спектральними термами.

Частота кожної спектральної лінії дорівнює різниці двох термів (78.5). Однак терм T (n)

для

інших атомів звичайно має більш складний вигляд, ніж для водневого атома. Крім того, перший і другий члени формули (78.5) беруться з різних рядів термів.

§ 79 Борівська теорія воднеподібного атома. Узагальнена формула Бальмера. Стала Рідберга. Недоліки теорії Бора [3]

1 Використовуючи постулати (Бора), умови квантування орбіт та деякі закони класичної механіки, Бор створив напівкласичну теорію воднеподібного атома. Розглянемо детально цю теорію.

Відповідно до моделі атома Резерфорда електрон у воднеподібному атомі рухається в

полі атомного ядра із зарядом Ze по колу під дією сили Кулона. При

Z = 1 така система

відповідає атому водню, при інших Z – воднеподібному іону, тобто атому з порядковим номером Z, у якого вилучені всі електрони, крім одного. В атомі електрон під дією сили Кулона рухається по коловій орбіті радіуса r зі швидкістю u з доцентровим прискоренням

aдоц = u

/ r. Рівняння другого закону Ньютона для електрона в цьому випадку має вигляд

u2

meaдоц = FК, або me

r

= 1

4pe0

Ze 2 r 2

. (79.1)

Також згідно з першим постулатом Бора електрон може рухатися тільки по

стаціонарних орбітах, для яких момент імпульсу електрона квантування орбіт задовольняє умову:

L = me u r

відповідно до правила

me u r = n h

(n = 1, 2, 3,...). (79.2)

Число n у виразі (79.1) називається головним квантовим числом, де me

u - його швидкість; r – радіус орбіти; h – стала Планка.

– маса електрона;

атомі.

Система рівнянь (79.1) (79.2) повністю описує поведінку електрона у воднеподібному

Виключивши швидкість u із рівнянь (79.1) і (79.2), отримаємо вираз для радіусів

стаціонарних орбіт:

r º r

= 4pe

h n 2

(n = 1, 2, 3,...). (79.3)

e

n 0 m Ze 2

Радіус першої орбіти (n = 1) атома водню (Z = 1) називається борівським радіусом. Його значення дорівнює

r 0= 0,529 ×10

-10

м. (79.4)

Відзначимо, що борівський радіус має порядок значення газокінетичних розмірів атома.

Внутрішня енергія атома складається з кінетичної енергії електрона (ядро є нерухомим) і енергії електростатичної взаємодії електрона з ядром:

E = me u

1 Ze 2

-.

З (79.1) випливає, що

2 4pe0 r

2 2

me u

= 1 1 Ze.

Отже,

2 2 4pe0 r

2 2 2

E = 1 Ze - 1 Ze = - 1 Ze.

8pe0 r

4pe0 r

8pe0 r

Підставивши сюди вираз (79.3) для r, знайдемо значення енергії атома на стаціонарних орбітах:

E º E

æ 1

= -ç

e

ö m Z

÷

2 e 4 1

(n = 1, 2, 3,...). (79.5)

n

ç 4pe0÷

2h2 n 2

è ø

Як бачимо, повна енергія воднеподібного атома визначається числом n. Саме тому число n

отримало назву головного квантового числа.

При переході атома водню (Z = 1

) зі стану n в стан m випромінюється фотон,

енергія якого визначається другим постулатом Бора

æ 1 ö

m e 4 æ 1 1 ö

e

hw = En - Em = -ç

÷ 2 ç 2 -

2 ÷.

è 4pe0ø

Частота випромінюваного світла дорівнює

2h è n m ø

E - E

æ 1 ö

m e 4 æ 1 1 ö

æ 1 1 ö

n m

e

w = = ç

÷ 3 ç

2 - 2 ÷ = R ç

2 - 2 ÷.

h è 4pe0ø

2h è m n ø

è m n ø

Ми прийшли до узагальненої формули Бальмера, причому для сталої Рідберга отримали значення

æ ö m e 4

R =  

e = 2,07 ×1016c-1. (79.6)

3

è 4pe0ø 2h

Як бачимо, при підстановці у вираз (79.6) числових значень

me, e і h отримуємо величину,

що дуже добре узгоджується з експериментальним значенням сталої Рідберга.

2 Теорія Бора була великим кроком у розвитку теорії атома. Вона пояснила ряд експериментальних фактів, стала потужним стимулом для проведення багатьох експериментальних досліджень, які принесли важливі результати. Навіть у тих випадках (а таких випадків була більшість), коли теорія не могла кількісно пояснити багато явищ, два постулати Бора були керівною ниткою при класифікації і якісній інтерпретації цих явищ. На їх основі, наприклад, був класифікований величезний емпіричний матеріал атомної й молекулярної спектроскопії.

Після перших успіхів теорії Бора усе чіткіше проявлялися її недоліки. Особливо тяжкою була невдача при побудові теорії атома гелію – одного з найпростіших атомів після атома водню.

Самою слабкою стороною теорії Бора була її внутрішня логічна суперечливість: вона

не була ні послідовно класичною, ні послідовно квантовою теорією. Після відкриття хвильових властивостей речовини стало зрозуміло, що теорія Бора, яка опирається на класичну механіку, є перехідним етапом на шляху до створення послідовної квантової теорії атомних явищ.

ТЕМА 14 ХВИЛЬОВІ ВЛАСТИВОСТІ МІКРОЧАСТИНОК

§ 80 Гіпотеза де Бройля. Довжина хвилі де Бройля для електрона, що вільно рухається [6, 11]

1 У результаті поширення уявлень про природу світла з'ясувалося, що світло виявляє корпускулярно хвильовий дуалізм (подвійність). В одних явищах проявляється його хвильова природа, і він веде себе як електромагнітна хвиля (інтерференція, дифракція), в інших явищах проявляється корпускулярна природа світла, і він веде себе як потік фотонів (фотоефект, явище Комптона).

У 1924 р. де Бройль висунув сміливу гіпотезу, що дуалізм не є особливістю тільки світла. Він припустив, що і частинки речовини поряд з корпускулярними властивостями мають також і хвильові (корпускулярно-хвильовий дуалізм частинок). Де Бройль переніс на частинки речовини такі самі правила переходу від корпускулярних характеристик до хвильових, які є справедливими у випадку світла.

Так відомо, що фотон світла має енергію

й імпульс

E = hw

(80.1)

p = 2ph / l, (80.2)

які пов’язані з частотою w та довжиною l світлової хвилі.

За гіпотезою де Бройля рух будь-якої частинки пов'язаний із хвильовим процесом, довжина хвилі визначається аналогічно до (80.2)

а частота – аналогічно до (80.1)

l = 2ph / p

(80.3)

w = E / h. (80.4)

Формули (80.3) та (80.4) визначають довжину та частоту хвилі де Бройля (хвилі,

що відповідає частинці речовини).

2 Все викладене вище є гіпотетичним і тому не має доказової сили. Точним доведенням або спростуванням отриманих результатів може бути тільки дослід. У яких саме явищах природи можуть виявитися хвильові властивості речовини, якщо вони дійсно існують? Незалежно від фізичної природи хвиль до таких явищ відносять інтерференцію й дифракцію. Безпосередньо величиною, яка тут досліджується, є довжина хвилі l. У всіх випадках довжини хвиль де Бройля визначаються формулою (80.3). Застосуємо її до

нерелятивістського руху частинок. Для електронів з масою

me, які прискорені різницею

потенціалів U, імпульс визначається із закону збереження енергії

p = me u

= eU,

тобто

Тоді з (80.3) отримаємо

2 me

p =

2 eUme. (80.5)

l = 2ph /

2 eUme. (80.6)

Визначимо довжину хвилі де Бройля для електронів, які прискорені напругою від 100 В до 10 кВ. Підставивши у співвідношення (80.6) відповідні числа, отримаємо, що довжина хвилі де Бройля такого електрона змінюється від 0,39 нм до 0,012 нм, тобто відповідає рентгенівському діапазону.

Таким чином, довжина хвилі де Бройля для електронів, які прискорені напругою від 100 В до 10 кВ, мають такий самий порядок, що й довжини хвиль рентгенівських променів. Тому дифракцію таких електронів потрібно намагатися шукати методами, аналогічними до тих, які застосовуються у випадку рентгенівських променів. Однак гіпотеза де Бройля уявлялась настільки фантастичною, що порівняно довго ніхто з експериментаторів не намагався піддати її експериментальній перевірці.

§ 81 Досліди Девісона й Джермера. Досліди Томсона й Тартаковського [3]

1 Гіпотеза де Бройля була підтверджена експериментально в дослідах Девісона й Джермера, а також Томсона (1927) та Тартаковського.

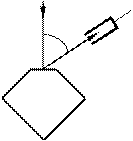Девісон і Джермер досліджували в 1927 р. відбиття

електронів від монокристала нікелю, що належить до кубічної системи. Вузький пучок моноенергетичних електронів спрямовувався на поверхню монокристала, який був відшліфований перпендикулярно до великої діагоналі кристалічної комірки. Відбиті електрони вловлювалися циліндричним електродом, який був приєднаним до гальванометра (рис. 81.1). Інтенсивність відбитого пучка оцінювалася за силою електричного струму, що проходить

j

Рисунок 81.1

До гальва- нометра

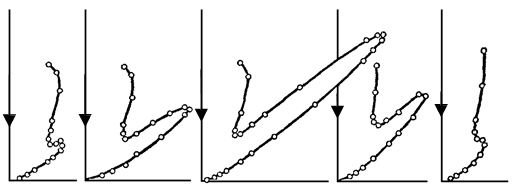
через гальванометр. Змінювалися швидкість електронів і кут j. На рис. 81.2 показана

залежність сили струму, яка вимірювалася гальванометром, від кута j при різних енергіях електронів.

Вертикальна вісь на графіках визначає напрям електронного пучка, що падає на

монокристал. Сила струму в заданому напрямку відображається довжиною відрізка, який проведено від початку координат до точки перетину з кривою. З рисунка бачимо, що розсіювання виявилося особливо інтенсивним при певному значенні кута j. Цей кут

відповідав відбиттю від атомних площин, відстань d між якими була відома з рентгенографічних досліджень. При даному j сила струму виявилася особливо значною при

прискорювальній напрузі, яка дорівнювала 54 В. Обчислена за формулою де Бройля довжина хвилі електрона

l = h =

p

h

2 meU

, (81.1)

яка відповідає цій напрузі, дорівнює 0,167 нм. Бреггівська довжина хвилі, що відповідає умові2(див. питання «Дифракція на просторових структурах. Закон Вульфа-Брегга»)

2 d sin q = m l

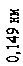дорівнювала 0,165 нм. Збіг цих довжин хвиль настільки вражаючий, що досліди Девісона й Джермера визнано блискучим підтвердженням ідеї де Бройля.

44 В 48 В 54 В 64 В 68 В

Рисунок 81.2

2 Г.П.Томсон (1927) і незалежно від нього

Фото-

П.С.Тартаковський отримали дифракційну картину

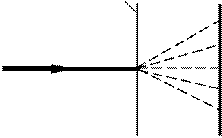при проходженні електронного пучка через металеву фольгу. Схема досліду подана на

рис. 81.3. Пучок електронів, прискорений

різницею потенціалів порядку декількох десятків кіловольт, проходив через тонку металеву фольгу

Пучок

Фольга

пластинка

й попадав на фотопластинку. Електрон при ударі

об фотопластинку відіграє таку саму роль, як і фотон. Отримана таким способом електронограма

золота (рис. 81.4 а) подібна до рентгенограми

електронів

Рисунок 81.3

алюмінію (рис. 81.4 б), яка отримана в аналогічних умовах. Подібність обох картин вражає. Штерн і його співробітники показали, що дифракційні явища мають місце також і для атомних та молекулярних пучків. У всіх перелічених випадках дифракційна картина відповідає довжині хвилі, яка визначається співвідношенням (81.1).

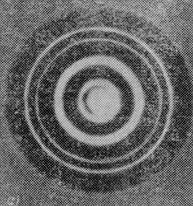
а б

Рисунок 81.4

2 Кут ковзання q пов’язаний з кутом j співвідношенням q = p - j.

2 2

§ 82 Статистична інтерпретація хвиль де Бройля [11]

Який же фізичний зміст хвиль де Бройля і який їх зв'язок із частинками речовини? Об’єкти мікросвіту є частинками, чи хвилями?

1 Одна з хибних гіпотез, за допомогою якої Шредінгер спробував відповісти на це питання, а потім швидко відмовився від неї, полягає у такому. Ніякого дуалізму хвиль і

частинок у дійсності не існує. Існують тільки хвилі. Частинки ж є суперпозицію хвиль. Справа в тому, що через математичну теорему Фур'є із хвиль різних частот і напрямків

завжди можна скласти хвильовий пакет, тобто таке хвильове утворення, що при накладенні в певний момент часу хвилі будуть підсилювати одна одну в деякій малій області простору, а

поза цією областю відбудеться їх повне гасіння. Такий хвильовий пакет і є частинка.

Інтенсивність хвиль де Бройля розглядається тут як величина, яка пропорційна густині середовища, з якої утворюється частинка. Здавалося, що підтвердженням такої точки зору є

та обставина, що центр хвильового пакета, подібно до центра групи хвиль, повинен у вакуумі

поширюватися із груповою швидкістю. А групова швидкість хвиль де Бройля і дорівнює швидкості частинки. Однак хвильовий пакет не може поводитися як частинка тривалий час. Причиною цього є те, що навіть у вакуумі хвилі де Бройля мають дисперсію. Внаслідок дисперсії такий хвильовий пакет буде еволюціонувати в часі. Монохроматичні хвилі різних частот, з яких утворений пакет, будуть розходитися з різними фазовими швидкостями. Це призведе до деформації, розпливання і зрештою до розпаду первісного хвильового пакета. Таким чином, частинка, якщо вона була хвильовим утворенням, була б нестійкою й швидко розпадалася б. Це жодною мірою не відповідає дійсності. Таким чином, частинка не може бути хвильовим пакетом, утвореним із хвиль де Бройля.

2 Не можна прийняти й протилежну точку зору: первинними є частинки, а хвилі

представляють їхні утворення, тобто виникають у середовищі, що складається із частинок, подібних до звуку, що поширюється у повітрі. Дійсно, таке середовище повинно бути досить щільним, тому що про хвилі в середовищі частинок має сенс говорити лише тоді, коли середня відстань між частинками є дуже малою у порівнянні з довжиною хвилі. А в типових випадках для хвиль де Бройля ця умова не виконується. Але якщо б навіть ми перебороли це утруднення, то все-таки зазначена точка зору повинна бути відкинута. Насправді вона означає, що хвильові властивості притаманні системам багатьох часток, а не окремим частинкам. Тим часом хвильові, інтерференційні властивості часток не зникають і при малих інтенсивностях падаючих пучків. Це було доведено прямими дослідами Бібермана, Сушкіна й Фабриканта з електронами. У дослідах Бібермана, Сушкіна й Фабриканта застосовувалися настільки слабкі пучки електронів, що середній проміжок часу між двома послідовними проходженнями електрона через дифракційну систему був приблизно в 30 000 разів більше часу, яке витрачається одним електроном на проходження всього приладу. За таких умов взаємодія між електронами, звичайно, не відіграла ніякої ролі. Тим часом при досить тривалій експозиції виникала дифракційна картина, яка нічим не відрізнялася від картини, що отримували при короткій експозиції з пучками електронів,

інтенсивність яких була приблизно у 107

разів більше. Важливим є те, що в обох випадках

загальне число електронів, які потрапили на фотопластинку, було однакове. Це показує, що й

окремі частинки мають хвильові властивості. Побічним доказом цього є також те, що хвильові властивості мають електрони атомних оболонок, наприклад, єдиний електрон атома водню, і при цьому про середовище, що утворене електронами, говорити не доводиться.

3 Так який же фізичний зміст хвиль де Бройля? Щоб відповісти на вищепоставлене

питання, розглянемо такий експеримент. Припустимо, що пучок частинок (для визначеності будемо говорити про електрони) падає на деякий дифракційний пристрій, наприклад кристал. Як показують експерименти, дифракція властива й хвилям де Бройля, що відповідають тільки одній частинці. Тому можна припустити, що у пучок, який падає, складається всього з одного електрона. При проходженні відповідної електронної хвилі де Бройля через кристал вона розбивається на кілька дифракційних пучків. Не можна припускати, що в кожному з таких пучків знаходиться якась частинка електрона.

Електрон діє завжди як ціле й ніколи не проявляється частина електрона, – у цьому проявляється атомізм, що властивий мікросвіту. Припустимо, що на шляху одного з дифрагованих пучків поставлений лічильник для вловлювання електронів. Якщо лічильник спрацьовує, то він завжди виявляє цілий електрон, а аж ніяк не його частину. Із цього не можна зробити висновок, що до виявлення електрон знаходився тільки в одному розглянутому дифрагованому пучку, а тому всі інші дифраговані пучки ніякої ролі не відіграли – їх просто не існувало. Така точка зору означала б, що електрон проходить через експериментальний пристрій як матеріальна точка класичної механіки. Це є несумісним з явищами інтерференції й дифракції електронів. Якщо повторити той самий дослід з іншим електроном, то електрон виявиться також в одному з дифрагованих пучків, але в загальному випадку не в тому самому. Подібні труднощі змусили Борна запропонувати статистичну інтерпретацію хвиль де Бройля, що дозволяє об’єднати атомізм частинок з їх хвильовими властивостями.

4 Відповідно до статистичної інтерпретації хвилі де Бройля потрібно розглядати як хвилі ймовірності. А саме: інтенсивність хвилі де Бройля в будь-якому місці простору пропорційна ймовірності виявити частинку в цьому місці. Але статистичні або імовірнісні властивості частинок можуть бути встановлені на досліді не з одною частинкою, а лише з багатьма частинками або тільки з однією частинкою, якщо дослід за певних умов повторений багаторазово. Говорити про статистику й імовірність має сенс лише стосовно певної сукупності елементів, до яких ці поняття відносять. Це може бути або сукупність багатьох одночасних елементів, які спостерігаються, або один елемент, який спостерігається у послідовні моменти часу. Такі сукупності елементів у квантовій механіці називаються квантовими ансамблями. Квантовий ансамбль, і це є одним з основних положень квантової механіки, реалізується шляхом встановлення деяких макроскопічних параметрів. Це, звичайно, не означає, що хвильові властивості властиві ансамблям частинок, а не самим частинкам. Ансамблі необхідні тільки для виявлення таких властивостей.

5 Як зі статистичної точки зору пояснюється дифракція частинок, наприклад

електронів? Перед влученням на дифракційний пристрій електрони проходять певну прискорювальну різницю потенціалів, якій відповідає одне і те саме значення довжини хвилі де Бройля. Прискорювальний потенціал і є тим макроскопічним параметром, що виділяє квантовий ансамбль частинок. Нехай реєстрація електронів виконується за допомогою фотопластинки. У яке місце фотопластинки потрапить індивідуальний електрон, достовірно передбачити неможливо; це можна зробити тільки з тим або іншим ступенем імовірності. Імовірність влучення електрона в те або інше місце фотопластинки пропорційне інтенсивності хвилі де Бройля в цьому місці. Окремий електрон залишає на фотопластинці (після її прояву) пляму. Якщо електронів мало, то фотопластинка буде нагадувати мішень, що прострелена невеликою кількістю куль. У розміщенні плям на фотопластинці не виявиться ніякої закономірності. Закономірність буде статистичною, коли на пластинку потрапить дуже багато електронів. У цьому випадку вони переважно потраплять у ті місця фотопластинки, де повинні бути дифракційні максимуми хвиль де Бройля. Сукупність відповідних плям і є дифракційною картиною, що отримується на досліді. Поки електростатичне відштовхування між електронами несуттєве, дифракційна картина буде однією й тією самою незалежно від того, чи утвориться вона електронами, що послідовно проходять по одному через прилад, або відразу інтенсивним пучком однаково прискорених електронів, який складається з такого самого числа частинок.

§ 83 Співвідношення невизначеностей Гейзенберга [11]

1 У класичній механіці стан матеріальної точки в довільний момент часу характеризується її положенням й імпульсом, тобто можна одночасно встановити їх точні значення координат та імпульсу. Для реальних мікрочастинок миттєвий стан не можна

характеризувати точними значеннями їх координат й імпульсу. Причина цього полягає у тому, що будь-яка мікрочастинка має як корпускулярні, так і хвильові властивості.

Не можна сказати, що в певній точці простору довжина хвилі дорівнює l, якщо про хвильове поле у всіх інших точках простору нічого не відомо. Довжина хвилі є

характеристикою синусоїди, а синусоїда – нескінченна періодична крива. Вираз «довжина хвилі в даній точці простору x дорівнює l» або «частота хвильового процесу в цей момент часу t дорівнює w» не мають ніякого змісту – величина l не є функцією x, а величина w – функцією t.

З іншого боку, якщо деяке хвильове утворення займає обмежену область простору, то його завжди можна подати синусоїдами. Тільки однієї синусоїди для цього недостатньо.

Необхідний хвильовий пакет – суперпозиція великої кількості синусоїд різних частот, які підсилювалися б у певному інтервалі простору й взаємно гасили б один одного поза цим

інтервалом. Якщо довжина хвильового пакета дорівнює D x

(заради простоти ми

обмежуємося одним виміром), то хвильові числа k, які необхідні для його утворення, не

можуть займати який завгодно вузький інтервал

D k. Мінімальна ширина інтервалу

хвильових чисел хвильового пакета задовольняти співвідношення

Це – чисто хвильове співвідношення.

D k, як доводять математики, повинна приблизно

D x × D k ³ 2p. (83.1)

Розглянемо тепер хвильовий пакет із хвиль де Бройля, розміри якого й відповідні межі хвильових чисел задовольняють умову (83.1). Відповідно до статистичної інтерпретації ймовірність виявлення частинки буде відмінна від нуля тільки в межах пакета. А чому буде дорівнювати імпульс частинки? Кожній хвилі де Бройля із хвильовим числом k відповідає

значення імпульсу

px = h k

(заради простоти ми розглядаємо випадок руху вздовж осі X).

Певного імпульсу для всього пакета не існує. Існує набір імпульсів, що заповнюють інтервал

px = h k до

px + D px = h(k + D k). Невідомо, який імпульс буде виявлений у хвильовому пакеті

при вимірі. У найкращому разі можна з’ясувати тільки його ймовірність. При вимірі імпульс

буде виявлений з тією або іншою ймовірністю між

px = h k

і px + D px = h(k + D k). Тому,

виражаючи k через

px, співвідношення (83.1) можна переписати у вигляді

D x × D px ³ 2ph = h. (83.2)

Це співвідношення називається співвідношенням або принципом невизначеностей Гейзенберга для координати й імпульсу частинки.

Співвідношення Гейзенберга визначає допустиму принципову межу неточностей D x

і D px, з якими стан частинки можна характеризувати класично, тобто координатою x й

імпульсом

px. Чим точніше x, тим з меншою точністю можливо характеризувати

px, і

навпаки. Але співвідношення Гейзенберга жодним чином не можна тлумачити у тому

розумінні, що частинка в кожний момент часу має певні значення x й

px, але ми їх

принципово не можемо визначити з більшою точністю, чим це дозволяє співвідношення невизначеностей (83.2). Така точка зору зовсім не відповідає природі досліджуваних мікрооб'єктів. Справжній зміст співвідношення (83.2) відображає той факт, що в природі

об'єктивно не існує станів частинок з точно визначеними значеннями обох змінних x і

px.

Принцип невизначеностей був сформульований Гейзенбергом у 1927 р. і став важливим кроком в інтерпретації закономірностей мікросвіту й побудові квантової механіки.

2 У тривимірному випадку класична частинка характеризується трьома прямокутними

координатами

x, y, z

й пов’язаними з ними імпульсами

px, py, pz. У цьому випадку

співвідношення невизначеностей Гейзенберга виражаються трьома нерівностями

D x × D px ³ h,

D y × D py ³ h,

D z × D pz ³ h. (83.3)

Ніяких обмежень на добутки типу

D x × D py, D y × D pz

співвідношення невизначеностей не

накладають. Величини x й

py, x і

pz одночасно можуть мати й зовсім точні значення.

3 Разом зі співвідношенням (83.1) у хвильовій теорії виводиться також формула

D t × Dw ³ 2p. (83.4)

Зміст цього співвідношення полягає в тому, що обмежений у часі хвильовий процес не може

бути монохроматичним. Якщо процес триває протягом часу

D t, то розкид частот Dw

хвиль,

якими цей процес характеризується, у н

Дата добавления: 2014-01-11